Neighbor Joining

The Neighbor-Joining algorithm is another quick clustering technique, which attempts to approximate the least squares tree, this time relying strongly on the additivity (and its implied corollaries) but without resorting to the assumption of a molecular clock. The idea here is to join clusters that are not only close to one another, but are also far from the rest. In each iteration, the algorithm attempts to find the direct ancestor of two species in the tree. For node i, its distance u_i from the rest of the tree is estimated using the formula: $u_i = \sum_{k \neq i}^{} \frac{D_{i,k}}{(n-2)}$. In order to minimize the sum of all branch lengths, also known as the minimum-evolution criterion, the nodes i and j that are clustered next are those for which D_i,j - u_i - u_j is smallest as can see in figure 8.10 (the reader is referred to [11] for a more elaborate explanation on this issue). The lengths d_k,(ij) of the new branches are calculated by solving the same system of linear equations mentioned earlier in section 8.3.1. The solutions are written below, in equations 8.8 and 8.9. Neighbor-Joining has a running time of O(n²), like UPGMA.

Neighbor-Joining algorithm [14]:

• Initialization: same as in UPGMA (see 8.3.5).
• Iteration:

  1.

    For each species, compute $u_i = \sum_{k \neq i}^{} \frac{D_{i,k}}{(n-2)}$.

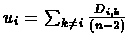  2.

  Choose the i and j for which D_i,j - u_i - u_j is smallest.

  3.

  Join clusters i and j to a new cluster - (ij), with a corresponding node in T. Calculate the branch lengths from i and j to the new node as:
  

  $$d_{i,(ij)} = \frac{1}{2}D_{i,j} + \frac{1}{2}(u_i - u_j)\ \ ,\ \ \ \ d_{j,(ij)} = \frac{1}{2}D_{i,j} + \frac{1}{2}(u_j - u_i)$$ (7)

  
  

  4.

  Compute the distances between the new cluster and each other cluster:
  

  $$D_{(ij),k} = \frac{D_{i,k} + D_{j,k} - D_{i,j}}{2}$$ (8)

  
  

  5.

  Delete clusters i and j from the tables, and replace them by (ij).

  6.

  If more than two nodes (clusters) remain, go back to 1. Otherwise, connect the two remaining nodes by a branch of length D_i,j.

  

Figure 8.10: D_i,j - u_i - u_j is the smallest, which means they are close to one anather and far from the rest of the tree, therefore the neighbor-joining algorithm will cluster them together.

lec08_figs/neighborjoin.ps