


Next: Neighbor Joining
Up: Distance Based Methods
Previous: Least Squares Methods
UPGMA
Being able to assign branch lengths to a given tree, as we have demonstrated, we
need to minimize SSQ(T) over the possible tree topologies. The UPGMA, or
Unweighted Pair Group Method with Arithmetic mean [13], is a
heuristic algorithm that usually generates satisfactory results. Basically, the
algorithm iteratively joins the two nearest clusters (or groups of species), until
one cluster is left.
UPGMA algorithm:
Let d be the distance function between species, we define the distance Di,j between two clusters of species Ci and Cj the following:
where ni = |Ci| and nj = |Cj|
- Initialization:
- 1.
- Initialize n clusters with the given species, one species per cluster.
- 2.
- Set the size of each cluster to 1:
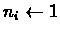 .
.
- 3.
- In the output tree T, assign a leaf for each species.
- Iteration:
- 1.
- Find the i and j that have the
smallest distance Dij.
- 2.
- Create a new cluster - (ij), which has
n(ij) = ni + nj members.
- 3.
- Connect i and j on the tree to a new node, which corresponds to the new
cluster (ij), and give the two branches connecting i and j to (ij) length
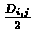 each.
each.
- 4.
- Compute the distance from the new cluster to all other clusters (except
for i and j, which are no longer relevant) as a weighted average of the distances from
its components:
- 5.
- Delete the columns and rows in D that correspond to clusters i and j,
and add a column and row for cluster (ij), with
D(ij),k computed as above.
- 6.
- Return to 1 until there is only one
cluster left.
Complexity: The time and space complexity of UPGMA is O(n2),
since there are n-1 iterations, with O(n) work in each one.
A clocklike, or ultrametric, tree is a rooted tree, in which the
total branch length from the root to any leaf is equal. In other words, there is a
``molecular clock'' that ticks in a constant pace (i.e., the mutation rate is
identical for all species), and all the observed species are at an equal number of
ticks from the root (see also page ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) ).
If the solution to the least squares problem is 0, and there is a molecular clock
(i.e., the solution is a clocklike tree), then UPGMA is guaranteed to return the
optimal solution. Actually, UPGMA implicitly assumes the
existence of an ultrametric tree, which explains why the new node, (ij), is the
mean of the two nodes that were joined to create it, as shown in figure
8.8.
It is therefore not surprising that for substantially non-clocklike trees, the algorithm
might give seriously misleading results.
).
If the solution to the least squares problem is 0, and there is a molecular clock
(i.e., the solution is a clocklike tree), then UPGMA is guaranteed to return the
optimal solution. Actually, UPGMA implicitly assumes the
existence of an ultrametric tree, which explains why the new node, (ij), is the
mean of the two nodes that were joined to create it, as shown in figure
8.8.
It is therefore not surprising that for substantially non-clocklike trees, the algorithm
might give seriously misleading results.
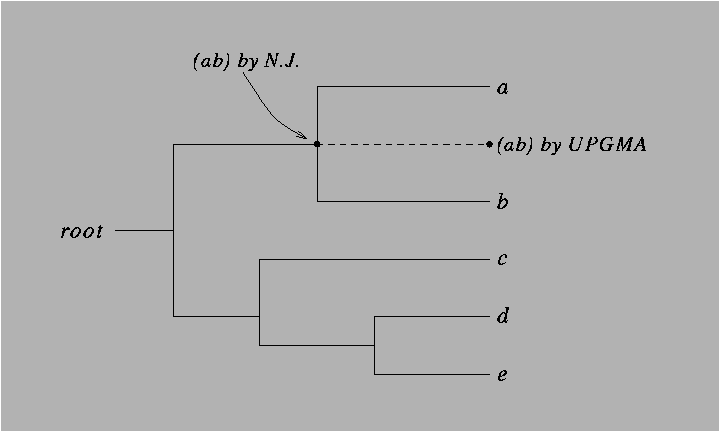
Figure 8.8:
A clocklike tree, showing the clustering (ab) of the
two nodes a and b by UPGMA and by the Neighbor-Joining
algorithm.
 |
Another assumption that UPGMA does is
additivity: In the "real"
tree, distances between species are the sum of distances along the path between the corresponding leaves.
There are two corollaries of additivity that the next algorithm will use
- For every three nodes i,j,k connected through an internal node
m with the distances:
d(i,m)=a, d(j,m)=b, d(k,m)=c then
dm,k=1/2(di,j+dj,k-di,j).
- For every four nodes i,j,k,l connected through an two internal
nodes m,n where m is connected with i,k and n, and nis connected with j,l and m then
di,k+dj,l <= di,j+dk,l = di,l+dk,j (see figure 8.9).
Figure 8.9:
di,j+dk,l <= di,j+dk,l = di,j+dk,l.
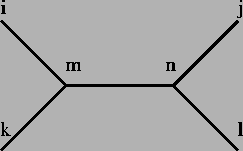 |



Next: Neighbor Joining
Up: Distance Based Methods
Previous: Least Squares Methods
Peer Itsik
2001-01-01
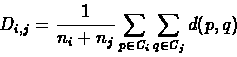
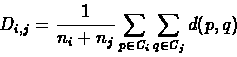
![]() ).
If the solution to the least squares problem is 0, and there is a molecular clock
(i.e., the solution is a clocklike tree), then UPGMA is guaranteed to return the
optimal solution. Actually, UPGMA implicitly assumes the
existence of an ultrametric tree, which explains why the new node, (ij), is the
mean of the two nodes that were joined to create it, as shown in figure
8.8.
It is therefore not surprising that for substantially non-clocklike trees, the algorithm
might give seriously misleading results.
).
If the solution to the least squares problem is 0, and there is a molecular clock
(i.e., the solution is a clocklike tree), then UPGMA is guaranteed to return the
optimal solution. Actually, UPGMA implicitly assumes the
existence of an ultrametric tree, which explains why the new node, (ij), is the
mean of the two nodes that were joined to create it, as shown in figure
8.8.
It is therefore not surprising that for substantially non-clocklike trees, the algorithm
might give seriously misleading results.
