Pairwise Distances

Given a measure of the distance between each pair of species, a simple approach to the phylogeny problem would be to find a tree that predicts the observed set of distances as closely as possible. This leaves out some of the information in the data matrix M, reducing it to a simple table of pairwise distances. However, it seems that in many cases most of the evolutionary information is conveyed in these distances.

For the analysis in this section, we shall first need to define an additive continuous distance function, so that the distance between two species would be expected to be proportional to the total branch lengths between the species. Thus if species a and b are connected via two edges in the tree, with lengths d_a,v and d_b,v (see figure 8.7), the distance between them would be d_a,v+d_b,v. Furthermore, given the distances between three species - d_a,b, d_a,c, and d_b,c, we could easily calculate the inner distances - d_a,v, d_b,v, and d_c,v, by solving a system of linear equations. Figure 8.7 illustrates a small tree, and table 8.2 contains the distances it predicts.

  

Figure 8.7: A small tree with 3 species - a, b, and c. The branch lengths correspond to the pairwise distances in table 8.2.

 

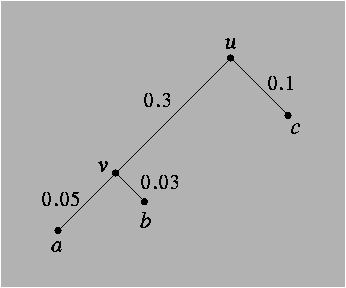Table 8.2: Distances d_i,j predicted by the tree in figure 8.7.

	a	b	c
a	0	0.08	0.45
b	0.08	0	0.43
c	0.45	0.43	0

 

We will give some examples of how distances may be computed to make them comply with our requirements - one for proteins, and another for DNA sequences.