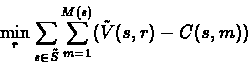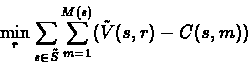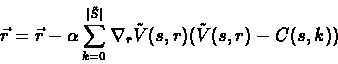Next: Evaluation Of Approximate Policy
Up: Approximate Policy Iteration
Previous: The algorithm using Monte
Solving the Least-Squares Problem
Let 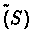 be a set of representative states, M(s) the number of samples of
be a set of representative states, M(s) the number of samples of
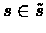 ,
the mth such sampled is denoted by c(s,m) and r is the vector parameter upon which the following optimisation problem is solved.
,
the mth such sampled is denoted by c(s,m) and r is the vector parameter upon which the following optimisation problem is solved.
The solution can be obtained by an incremental algorithm, which performs steps in the gradient direction.We will have the following equation for a certain run
(s1,a1,....,sn).
Yishay Mansour
2000-01-11