Solving the Unique Mapping Problem Using Interval Graphs

Create a graph G(V,E) whose vertices are the clones, and its edges are 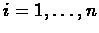$E=\{(v_{i},v_{j})\vert$ there exists a probe p, $p(v_{i}) = p(v_{j})\}$   A graph G(V,E) is said to be an interval graph if every node can be represented as an interval and an edge exists between two vertices if and only if the intervals corresponding to them overlap. The set of such intervals is then called a realization of G.
 
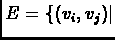
Intuitively, it is clear that the problem of checking if a graph is an interval graph is closely related to 9.1 (finding $\Pi(\varphi)$). The problem of recognition of interval graphs can be solved in polynomial time [1]. The algorithm is based on a following theorem:
 
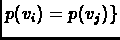
To solve the problem mentioned above a matrix is created displaying the connection between the maximal cliques and the vertices:

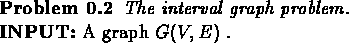$$M_{i,j} = \begin{array}{cc} 1 & \mbox{if vertex $i$\space is in clique $j$ }, \\ 0 & \mbox{otherwise}. \end{array}$$ (1)

By using the algorithm of [1] given in section 9.1.3, we try to find a permutation on the clique order satisfying the requirements of theorem 9.2, furthermore, such a permutation allows easy computation of a set of intervals corresponding to the nodes. Note that the construction of the matrix M above uses the following property: An interval graph has O(n) maximal cliques and these cliques can be found in O(n) time. As mentioned above, solving the unique mapping problem can be done quite easily using PQ-trees in the absence of noise. In the case of either missing edges (probe not identified) or extra edges (probe identified where it should not have been) the resulting graph might not be an interval graph. The problem of creating an interval graph from the existing graph is known as the interval graph editing problem. Slight modifications introduce other variants like the interval graph sandwich problem.