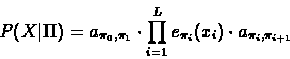Hidden Markov Models

A path $\Pi=(\pi_{1},\ldots,\pi_{L})$ in the model $\mathcal{M}$ is a sequence of states. We can now define the state transition probabilities and the emission probabilities in terms of $\Pi$ given a sequence $X = (x_{1},\ldots,x_{L}) \in \Sigma^{\ast}$:

$$\begin{split} &a_{kl} = P(\pi_{i}=l \vert \pi_{i-1}=k) \\ &e_{k}(b) = P(x_{i}=b \vert \pi_{i}=k) \end{split}$$ (6.6)

The probability that the sequence X was generated by the model $\mathcal{M}$ given the path $\Pi$ is therefore:

$$P(X\vert\Pi) = a_{\pi_{0},\pi_{1}} \cdot \prod_{i=1}^{L} {e_{\pi_{i}}(x_{i}) \cdot a_{\pi_{i},\pi_{i+1}}}$$ (6.7)

Where for our convenience we denote $\pi_{0} = begin$ and $\pi_{L+1} = end$.

Example 6.3   An HMM for detecting CpG islands in a long DNA sequence.

The model contains eight states corresponding to the four symbols of the alphabet $\Sigma=${A,C,G,T}:

State:	A+	C+	G+	T+	A-	C-	G-	T-
Emitted Symbol:	A	C	G	T	A	C	G	T

If the probability for staying in a CpG island is p and the probability of staying outside it is q, then the transition probabilities will be as described in table 6.2 (derived from the transition probabilities given in table 6.1 under the assumption that we lose memory when moving from/into a CpG island, and that we ignore background probabilities).

 

Table 6.2: Transition probabilities in the CpG islands HMM

$a_{\pi_{i},\pi_{i+1}}$	A+	C+	G+	T+	A-	C-	G-	T-
A+	0.180p	0.274p	0.426p	0.120p	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$
C+	0.171p	0.368p	0.274p	0.188p	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$
G+	0.161p	0.339p	0.375p	0.125p	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$
T+	0.079p	0.355p	0.384p	0.182p	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$	$\frac{1-p}{4}$
A-	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	0.300q	0.205q	0.285q	0.210q
C-	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	0.322q	0.298q	0.078q	0.302q
G-	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	0.248q	0.246q	0.298q	0.208q
T-	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	$\frac{1-q}{4}$	0.177q	0.239q	0.292q	0.292q

 

In this special case the emission probability of each state X⁺ or X^- is exactly 1 for the symbol X and 0 for any other symbol.
Let us consider another example, where the emission probabilities will not be degenerate.

Example 6.4   Suppose a dealer in a casino tosses a coin. We know the dealer may use a fair coin or a biased coin which has a probability of 0.75 to get a "head". We also know that the dealer does not tend to change coins - this happens only with a probability of 0.1. Given a sequence of coin tosses we wish to determine when did the dealer use the biased coin and when did he use a fair coin.

The corresponding HMM is:

• The states are $Q = \{F,B\}$, where F stands for "fair" and B for "biased".
• The alphabet is $\Sigma = \{h,t\}$, where h stands for "head" and t for "tails".
• The probabilities are:
  

  a_FF = a_BB = 0.9 (6.8)

  a_FB = a_BF = 0.1 (6.9)

  
  
  
  

  $$\quad$$ e_F(h) = 0.5 e_F(t) = 0.5 (6.10)

  $$\quad$$ e_B(h) = 0.75 e_B(t) = 0.25 (6.11)

  
  

Figure 6.1 gives a full description of the model.

  

Figure 6.1: HMM for the coin tossing problem

Returning to the general case, we have defined the probability $P(X\vert\Pi)$ for a given sequence X and a given path $\Pi$. However, we do not know the actual sequence of states $(\pi_{1},\ldots,\pi_{L})$ that emitted $(x_{1},\ldots,x_{L})$. We therefore say that the generating path of X is hidden.

Problem 6.5   The decoding problem.
INPUT: A hidden Markov model $\mathcal{M}$ $= (\Sigma,Q,\Theta)$ and a sequence $X \in \Sigma^{\ast}$.
QUESTION: Find an optimal generating path $\Pi^{*}$ for X, such that $P(X\vert\Pi^{*})$ is maximized. We denote this also by:

$$\Pi^{*} = \arg\max_{\Pi}\{P(X\vert\Pi)\}$$

In the CpG islands case (problem 6.2), the optimal path can help us find the location of the islands. Had we known $\Pi^{*}$, we could have traversed it determining that all the parts that pass through the "+" states are CpG islands.
Similarly, in the coin-tossing case (example 6.4), the parts of $\Pi^{*}$ that pass through the B (biased) state are suspected tosses of the biased coin.
A solution for the optimal path problem is described in the next section.