The Overlap Graph

$\begin{definition}{The {\em overlap graph} of a permutation $\pi$ , denoted by $... ... reserving the names {\em node} and {\em arc} for $OV(\pi)$ ).} \end{definition}$

In other words, the node set of $OV(\pi )$ is the set of gray edges in $B(\pi )$ , and two nodes are connected by an arc if the intervals associated with their gray edges overlap. We shall identify a node in $OV(\pi )$ with the edge it represents and with its interval in the representation. Thus, the endpoints of a gray edge are actually the endpoints of the interval representing the corresponding node in $OV(\pi )$ . A connected component of $OV(\pi )$ that contains an oriented edge is called an oriented component, otherwise, it is called an unoriented component. Figure 10.10(c) shows the interval overlap graph for $\pi = (4,-3,1,-5,-2,7,6)$ . It has only one oriented component. Figure 10.11(b) shows the overlap graph of the permutation $\pi '=(4,-3,1,2,5,7,6)$ , which has two connected components, one oriented and the other unoriented.

**Figure:** (a) The breakpoint graph, $B'(\pi ')$ of $\pi '=(4,-3,1,2,5,7,6)$ . $\pi '$ was obtained from $\pi$ of figure 10.10 by the reversal $\rho (7,10)$ ; or, equivalently, by the reversal defined by the gray edge (2,3). (b) The overlap graph of $\pi '$ .
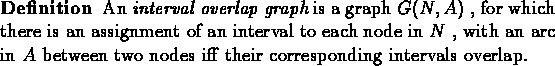$\includegraphics{lec10_fig/lec10_badmove1.eps}$

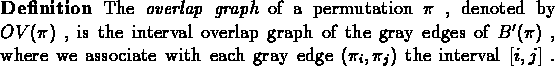
$\begin{lemma}The reversal acting on a gray edge flips the orientation of all edges overlapping it, leaving all other edges unchanged. \end{lemma}$

$\begin{lemma}A reversal acting on a gray edge is good iff the edge is oriented. \end{lemma}$

We shall see that any connected component which is oriented can be transformed by a series of reversals to a set of trivial connected components that correspond to the identity permutation. The unoriented connected components pose us a problem since we cannot split any of their cycles, nor delete any of their breakpoints by applying a single reversal.

In some cases we can eliminate unoriented components. This is done either by applying a reversal that does not increase the number of cycles, but rather transforms some of the edges to oriented edges, or by applying a reversal that merges two or more unoriented connected components into one oriented component.

The above idea for eliminating unoriented components allows a characterization of the unoriented components, on which we have to spend an extra reversal operation. We denote these components as hurdles.