


Next: Problem of sampling
Up: Evaluating One Policy With
Previous: Importance Sampling
Policy Sampling
The conclusion from the above equivalence is that if we can compute
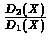 then we
then we
able to "transform"
samples from distribution D1 to samples in distribution D2.
We produce
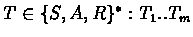 of policy
of policy 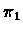 .
each sample(Tj) is a run on the model using policy
.
each sample(Tj) is a run on the model using policy 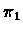 ,
i.e.
Tj = s1,a1,r1,s2,a2,r2...
,
i.e.
Tj = s1,a1,r1,s2,a2,r2...
The probability of generating Tj is actually a product of two independent
probabilities:
a policy depeneded probablity on actions and a model depended probability.
Prob[Tj] =
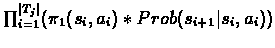 =
=
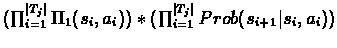
We calculte the ratio of probabilites to have the same Tj on differnt policies:
![$\frac{Prob_{\pi_{2}}[T_{j}]}{Prob_{\pi_{1}}[T_{j}]} =
\frac {(\prod_{i=1}^{\v...
...\prod_{i=1}^{\vert T_{j}\vert}\frac{\pi_{2}(s_{i},a_{i})}{\pi_{1}(s_{i},a_{i})}$](img24.gif)
The important fact is that the ratio does not depened on the model, but only on
the policies. Therefor we can compute it with out the model.
EXAMPLE 2
Input:
- policy
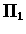 .
.
- policy
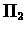 is determinstic.
is determinstic.
Computation:
- because
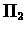 is determinstic
is determinstic
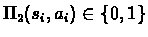
- Therefor the ratio is a product of X,
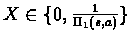
- If
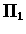 is the random policy than we simply have a uniform distribution on the
runs. Consistent with
is the random policy than we simply have a uniform distribution on the
runs. Consistent with 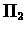 .
.
Yishay Mansour
2000-01-07
![$\frac{Prob_{\pi_{2}}[T_{j}]}{Prob_{\pi_{1}}[T_{j}]} =
\frac {(\prod_{i=1}^{\v...
...\prod_{i=1}^{\vert T_{j}\vert}\frac{\pi_{2}(s_{i},a_{i})}{\pi_{1}(s_{i},a_{i})}$](img24.gif)