Next: Program Up: Project Home Previous: Introduction

Theory of Wiener Filtering

The Wiener Filter is a noise filter based on Fourier iteration. its main advantage is the short computational time it takes to find a solution.

Consider a situation such that there is some underlying, uncorrupted singal u(t) that is required to measure. Error occur in the measurement due to imperfection in equipments, thus the output signal is corrupted. There are two ways the signal can be corrupted: First, the equipment can convolve, or 'smear' the signal. This occurs when the equipment doesn't have a perfect, delta function response to the signal. Let s(t) be the smear signal and r(t) be the known response that cause the convoltion. Then s(t) is related to u(t) by:

\begin{displaymath}s(t) = \int_{-\infty}^{\infty} r(t-\tau)u(\tau) \,d\tau.\end{displaymath}       or       S(f) = R(f)U(f)

(1)

where S, R, U are Fourier Transform of s, r, and u.

The second source of signal corruption is the unknown background noise n(t). Therefor the measured signal c(t) is a sum of s(t) and n(t):

c(t) = s(t) + n(t)

(2)

To deconvolve s to find u, simply divide S(f) by R(f), i.e. $ U(f) = \frac{S(f)}{R(f)} $ in the absense of noise n. To deconvolve c where n is present then one need to find an optimum filter function $\phi(t)$, or $\Phi(f)$, which filters out the noise and gives a signal $\tilde{u}$ by:

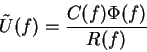
\begin{displaymath}\tilde{U}(f) = \frac{C(f)\Phi(f)}{R(f)} \end{displaymath}

(3)

where $\tilde{u}$ is as close to the original signal as possible.

For $\tilde{u}$ to be similar to u, their differences squared is as close to zero as possible, i.e.

\begin{displaymath}\int_{-\infty}^{\infty} \left\vert \tilde{u}(t) - u(t) \right\vert^2 \,dt \end{displaymath}      or      \begin{displaymath}\int_{-\infty}^{\infty} \left\vert \tilde{U}(f) - U(f) \right\vert ^2 \,df \end{displaymath}      is minimised

(4)

Substituting equation (1), (2) and (3), the Fourier version becomes:

\begin{displaymath}\int_{-\infty}^{\infty} \left\vert R(f) \right\vert^{-2} \lef... ...f) \right\vert^2 \left\vert \Phi(f) \right\vert^2 \right} \,df \end{displaymath}

(5)

after rearranging. The best filter is one where the above integral is a minimum at every value of f. This is when,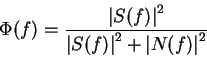

\begin{displaymath}\Phi(f) = \frac { \left\vert S(f) \right\vert^2 } { \left\vert S(f) \right\vert^2 + \left\vert N(f) \right\vert^2 } \end{displaymath}

(6)

Now, $ \left\vert S(f) \right\vert^2 + \left\vert N(f) \right\vert^2 \approx \left\vert C(f) \right\vert^2 $ where $ \left\vert C(f) \right\vert^2 $, $ \left\vert S(f) \right\vert^2 $ and $ \left\vert N(f) \right\vert^2 $ are the power spectrum of C, S, and N. Therefore,

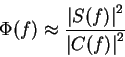
\begin{displaymath}\Phi(f) \approx \frac { \left\vert S(f) \right\vert^2 } { \left\vert C(f) \right\vert ^2 } \end{displaymath}

Figure 1 shows a plot of $ \left\vert C(f) \right\vert^2 $. It can be seen that $ \left\vert S(f) \right\vert^2 $ and $ \left\vert N(f) \right\vert^2 $ can be extrapolated from the graph.


Figure 1. Plot of power spectrum of signal plut noise

From the above theory, it can be seen that a program can be written to Wiener Filter signal from noise using Fourier Transform. This is what Jean is investigating with her part. There is another way to Wiener Filtering a signal but this time without Fourier Transform the data. The latter is what I set out to do with my part of programming, and this is the Mean-Squared Method.

 

The Mean-Squared Method

The Mean-squared Methods uses the fact that the Wiener Filter is one that is based on the least-squared principle, i.e. the filter minimises the error between the actual output and the desired output. To eliminate noise, this filter works by narrow the width of the distribution curve of figure 1.

To do this, first the varience of the data matrix is to be found. Then, a box of certain size is passed around the matrix, moving one pixel at a time. For every box, the local mean and variance is found. And the filtered value of each pixel is found by the following formula:

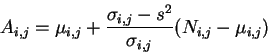
\begin{displaymath}A_{i,j} = \mu_{i,j} + \frac {\sigma_{i,j} - s^2} {\sigma_{i,j}} (N_{i,j} - \mu_{i,j}) \end{displaymath}

where Ai,j is the filtered signal, $\mu_{i,j}$ is the local mean, $\sigma_{i,j}$ is the local variance, s2 is the noise variance of the entire data matrix, and Ni,j is the original signal value.

From the above formula, it can be see that if the original signal is similar to the local varience then the filtered value will be that of the local mean, if the original signal is very much different from the local mean, then it will be filtered to give a higher/lower intensity signal depends on the differences. Also, if the local variance is similar to the matrix variance, which is around 1 (i.e. only noise exist in the box) then the filtered signal will be that of the local mean, which should be close to zero. But if the local variance is much bigger than the matrix variance (i.e. when the box is at the actual signal), then the signal will be amplified.

As the box moves through the entire matrix, it will calculate the solution to each pixel using the above formula, and thus filters the data. The program for the routine is shown in the next section: Program.

 

Next: Program Up: Project Home Previous: Introduction

Rosalind Wang
2000-05-27

My home page | SC3 home page | WebCT | Vislab home page
Competence1 | Competence2 | Competence3 | Competence4 | Project

Mail me