

Next: Background on the number
Up: Analysis of Bernstein's Factorization
Previous: Analysis of Bernstein's Factorization
Introduction
In [1], a new circuit-based approach is proposed for one of
the steps of the number field sieve (NFS) integer factorization
method, namely finding a linear relation in a large but sparse matrix.
Unfortunately, the proposal from [1] has been
misinterpreted on a large scale, even to the extent that announcements
have been made that the results imply that common RSA key sizes no
longer provide an adequate level of security.
In this paper we attempt to give a more balanced interpretation
of [1]. In particular, we show that 1024-bit RSA keys are as
secure as many believed them to be. Actually, [1] provides
compelling new evidence that supports a traditional and widely
used method to evaluate the security of RSA moduli. We present a variant
of the analysis of [1] that would suggest that, under the metric
proposed
in [1], the number of digits of factorable integers 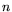 has grown
by a factor
has grown
by a factor 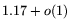 , for
, for
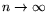 (in [1] a factor of
(in [1] a factor of 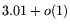 is mentioned).
We propose an improved circuit design, based on mesh routing
rather than mesh sorting. To this end we describe a new routing algorithm
whose
performance in our setting seems optimal. With some further optimizations,
the construction cost is reduced by several orders of magnitude compared
to [1]. In the improved design the parallelization is gained
essentially
for free, since its cost is comparable to the cost of RAM needed just
to store the input matrix.
We estimate the cost of breaking 1024-bit RSA with current technology.
Using custom-built hardware to implement the improved circuit,
the NFS matrix step becomes surprisingly inexpensive. However,
the theoretical analysis shows
that the cost of the relation collection step cannot be significantly
reduced, regardless of the cost of the matrix step. We thus conclude
that the practical security of RSA for commonly used modulus sizes is
not significantly affected by [1].
Section 2 reviews background on the NFS; it does not contain
any new material and simply serves as an explanation and confirmation of the
analysis from [1]. Section 3 sketches the circuit
approach of [1] and considers its implications.
Section 4 discusses various cost-aspects of the NFS.
Section 5 focuses on 1024-bit numbers, presenting custom
hardware for the NFS matrix step both following [1] and using the newly
proposed circuit. Section 6 summarizes our conclusions.
Appendices A and B outline the limitations
of off-the-shelf parts for the mesh-based approach and the
traditional approach, respectively.
Throughout this paper,
is mentioned).
We propose an improved circuit design, based on mesh routing
rather than mesh sorting. To this end we describe a new routing algorithm
whose
performance in our setting seems optimal. With some further optimizations,
the construction cost is reduced by several orders of magnitude compared
to [1]. In the improved design the parallelization is gained
essentially
for free, since its cost is comparable to the cost of RAM needed just
to store the input matrix.
We estimate the cost of breaking 1024-bit RSA with current technology.
Using custom-built hardware to implement the improved circuit,
the NFS matrix step becomes surprisingly inexpensive. However,
the theoretical analysis shows
that the cost of the relation collection step cannot be significantly
reduced, regardless of the cost of the matrix step. We thus conclude
that the practical security of RSA for commonly used modulus sizes is
not significantly affected by [1].
Section 2 reviews background on the NFS; it does not contain
any new material and simply serves as an explanation and confirmation of the
analysis from [1]. Section 3 sketches the circuit
approach of [1] and considers its implications.
Section 4 discusses various cost-aspects of the NFS.
Section 5 focuses on 1024-bit numbers, presenting custom
hardware for the NFS matrix step both following [1] and using the newly
proposed circuit. Section 6 summarizes our conclusions.
Appendices A and B outline the limitations
of off-the-shelf parts for the mesh-based approach and the
traditional approach, respectively.
Throughout this paper, 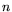 denotes
the composite integer to be factored. Prices are in US dollars.
denotes
the composite integer to be factored. Prices are in US dollars.


Next: Background on the number
Up: Analysis of Bernstein's Factorization
Previous: Analysis of Bernstein's Factorization