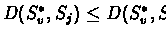Lifted Alignment tree - a Heuristic for Phylogenetic Alignment

Definition 5.13   A phylogenetic alignment is called lifted alignment if for every internal node v, the string assigned to v is also assigned to one of v's children (See figure 5.2). Trivially, in such a case, all internal nodes are assigned labels from the set of leaf strings.

Let T^* be the optimal alignment for tree T. We will construct a lifted alignment T^L = Lift(T^*), which is based on T^*, with only a limited damage to the alignment distance. Note that this construction is only conceptual since we usually do not know T^*. For each node v let its T^* label be S^*_v. We shall assign every v a label S^L_v. Initially, only the leaves are labeled, and by definition S^L_v = S^*_v for each leaf v. The labeling process successively traverses the internal nodes in any order, provided that a node is not visited before any of its children. Upon visiting a node, it is lifted i.e. labeled by one of the labels of its children. Thus, the resulting phylogenetic alignment is lifted. (see figure 5.3)

                            Procedure Lift(T : Tree)

 begin

		 while there
exists an unlifted node v, all of whose children have been
lifted, do :


Find a child j whose label Sj is the
closest to S*v. Namely


For every child i of
v:

		 		 		 		 $D(S^{*}_{v}, S_j) \leq D(S^{*}_{v}, S_i)$


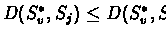
Label S*v with Sj


		 end while

 end 

  

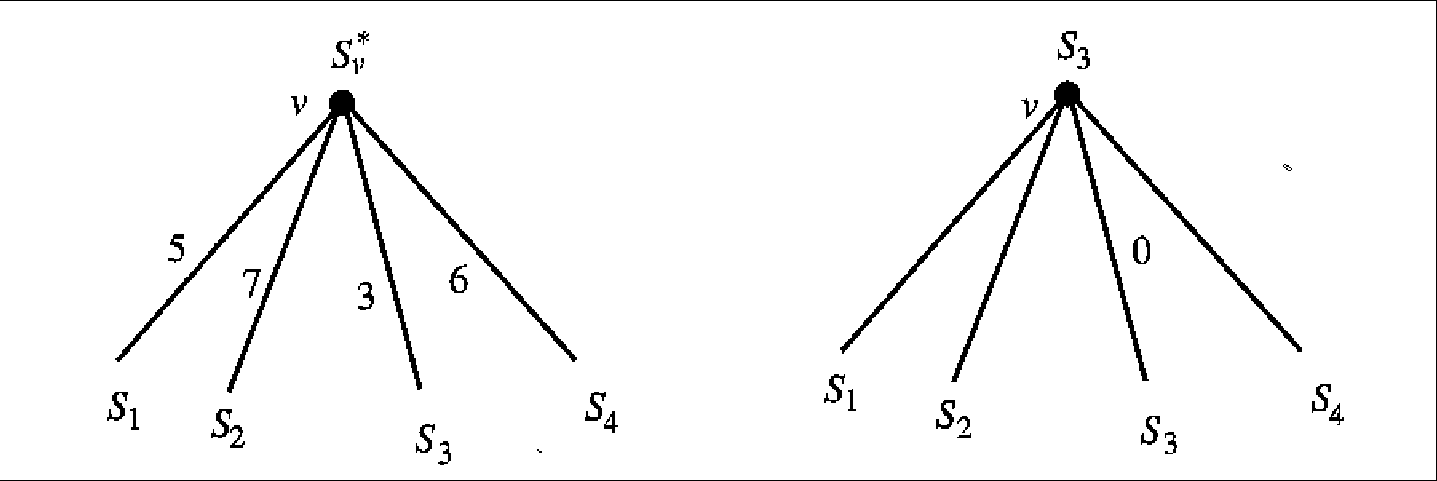
Figure 5.3: The lifting construction at node v. The numbers on the edges are the distances from S^*_v to the lifted strings labeling its children. On the left is the tree before lifting, and on the right the result of the lift. After the lift one edge will have a distance of 0.

Theorem 5.7 (Jiang, Wang and Lawler, 1996 [5])   The distance of the phylogenetic alignment T^L = Lift(T^*) is at most twice the distance of the optimal phylogenetic alignment T^*.

Proof:Let e = (v,w) be an edge in T. Suppose that in T^L, S_j is the label of v and S_i is the label of w. If i=j then D(S_j, S_i) = 0. Otherwise:

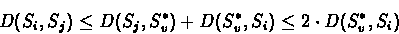$$D(S_i, S_j) \leq D(S_j,S^{*}_{v}) + D(S^{*}_{v}, S_i) \leq 2\cdot D(S^{*}_{v}, S_i)$$ (5.8)

The first inequality is due to the triangle inequality, and the second follows from the labeling algorithm. For an edge e = (v,w), with S_w = S_i ,Let P_e be the path in T from v to the leaf labeled S_i. Due to the triangle inequality

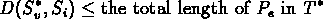$$D(S^{*}_{v}, S_i) \leq \mbox{the total length of $P_e$\space in } T^*$$ (5.9)

We say that the edge e = (v,w) is blue in T^L if 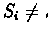$S_i \neq S_j$. The distance of a lifted alignment T^L is equal to the sum of edge distances on all the blue edges in the tree.
For a blue edge e = (v,w), observe that the definition of lifted alignment implies that along the path P_e every node except v is labeled S_i, and no node outside P_e is labeled S_i. Hence, if e' = (v', w') is any other blue edge, then P_e and P_e' have no edges in common. This defines a mapping from every blue edge e in T^L to a path P_e in T^* such that:

• The distance in T^L of the edge e is at most twice the total distance in T^* of the edges on P_e. (Follows from equations 5.8 and 5.9.
• No edge in T^* is mapped to by more than one edge in T^L.

Therefore the total distance of T^L = the total distance on blue edges $\leq$ $2 \cdot$ the sum of all total distances of P_e paths in T^* $\leq$ $2 \cdot$ the total distance of T^*. (see figure 5.4)

  

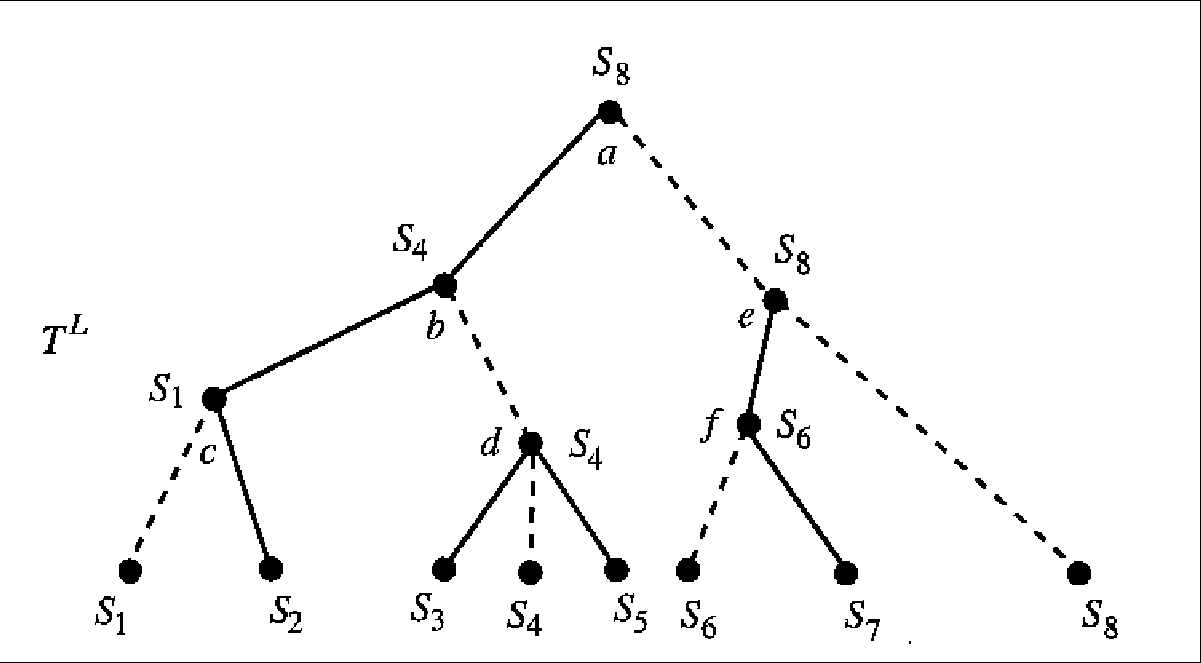
Figure 5.4: The lifted tree T^*_L. The dashed edges show the paths along which a leaf string has been lifted to some internal node. Solid edges are blue edges in T^*_L, while each of these dashed edges has distance 0. The path P_(a,b) for example, is the path b,d, S₄ along which the string labeling b was lifted. Edge (a,b) has distance in T^*_L at most twice the distance of path P_(a,b) in T^*.

We now describe how to find the optimal lifted alignment using a dynamic programming algorithm as listed below. But first we define:

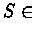
Definition 5.14   Let T_v be the subtree of T rooted at node v and $S \in \S$. Let d(v,S) denote the distance of the best lifted alignment of T_v under the requirement that string S is assigned to node v.

The algorithm will compute d(v,S) for any 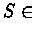$S \in \S$ working it's way from the leaves up using the following recursion:

• If v is an internal node with all its children being leaves, then 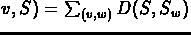$d(v,S) = \sum_{(v,w)} D(S, S_w)$ where S_w is the label of w.
• Else, $d(v,S) = \sum_{(v,v')} min_{S' \in S} [D(S,S') + d(v',S')]$ where v' is a child of v and S' is a label of one of the leaves of T_v'.

Time analysis: We perform a preprocessing stage, in which we compute all the $k \choose 2$ pairwise distances between the k input strings. This takes O(N²) time, where N is the total length of all the strings. The work at any internal node is O(k²), and the overall work of the algorithm is O(N² + k³)