PAM matrices

PAM matrices are amino acid substitution matrices that encode the expected evolutionary change at the amino acid level. Each PAM matrix is designed to compare two sequences which are a specific number of PAM units apart. For example - the PAM120 score matrix is designed to compare between sequences that are 120 PAM units apart: The score it gives a pair of sequences is the (log of the) probabilities of such sequences evolving during 120 PAM units of evolution. For any specific pair (A_i, A_j) of amino acids the (i,j) entry in the PAM n matrix reflects the frequency at which A_i is expected to replace with A_j in two sequences that are n PAM units diverged. These frequencies should be estimated by gathering statistics on replaced amino acids.

Collecting statistics about amino acids substitution in order to compute the PAM matrices is relatively difficult for sequences that are distantly diverged, as mentioned in the previous section. But for sequences that are highly similar, i.e., the PAM divergence distance between them is small, finding the position correspondence is relatively easy since only few insertions and deletions took place. Therefore, in the first stage statistics were collected from aligned sequences that were believed to be approximately one PAM unit diverged and the PAM1 matrix could be computed based on this data, as follows: Let M_ij denote the observed frequency (= estimated probability) of amino acid A_i mutating into amino acid A_j during one PAM unit of evolutionary change. M is a $20 \times 20$ real matrix, with the values in each matrix column adding up to 1. There is a significant variance between the values in each column. For example, see figure 3.1, taken from [4].

  

Figure: The top left corner $5 \times 5$ of the PAM1 matrix. We write 10⁴M_ij for convinience.

Once M is known, the matrix Mⁿ gives the probabilities of any amino acid mutating to any other during n PAM units. The (i,j) entry in the PAM n matrix is therefore:

$$\log \frac{f(j)M^{n}(i,j)}{f(i)f(j)} = \log \frac{M^{n}(i,j)}{f(i)}$$

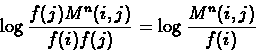
where f(i) and f(j) are the observed frequencies of amino acids A_i and A_j respectively. This approach assumes that the frequencies of the amino acids remain constant over time, and that the mutational processes causing substitutions during an interval of one PAM unit operate in the same manner for longer periods. We take the log value of the probability in order to allow computing the total score of all substitutions using summation rather than multiplication. The PAM matrix is usually organized by dividing the amino acids to groups of relatively similar amino acids and all group members are located in consecutive columns in the matrix.