


Next: Alignment Graph
Up: Global Alignment in linear
Previous: Global Alignment in linear
The Algorithm:
- 1.
- Compute V(A, B) while saving the values of the
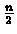 -th row. Denote D(A,B) as the Forward Matrix F.
-th row. Denote D(A,B) as the Forward Matrix F.
- 2.
- Compute V(Ar, Br) while saving the
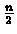 -th row. Denote
D(Ar, Br) as the Backward Matrix B.
-th row. Denote
D(Ar, Br) as the Backward Matrix B.
- 3.
- Find the column k* so that the crossing point (
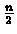 ,
k*) satisfies:
,
k*) satisfies:
- 4.
- Now that k* is found, recursively partition the problem to two sub problems:
(i) Find the path from (0,0) to (
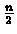 ,
k*).
,
k*).
(ii)
Find the path from (n, m) to (
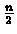 ,
m - k*).
,
m - k*).
Lemma 2.11
Time complexity of
Hirschberg's algorithm is
O(
nm).
Proof:Time complexity
Let
T*(n,m) = Time to find the value
of a
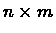 problem. Let T(n,m) = Time to find the path
(solution) of a
problem. Let T(n,m) = Time to find the path
(solution) of a
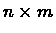 problem.
problem.
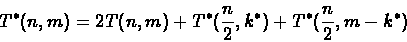 |
(2.1) |
T(n,m)=cnm, therefore
T*(n,m) = 4T(n,m) = 4cnm. according
to 2.1:
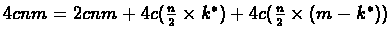 .
Therefore,
the time complexity will remain O(nm).
.
Therefore,
the time complexity will remain O(nm).
Lemma 2.12
Space complexity of
Hirschberg's algorithm is
O(
m)
Proof:Space Complexity
Each Dynamic Programming computation
requires storing one additional row (middle one) which can be
discarded once the middle point is found. Therefore the space
complexity will be O(m).



Next: Alignment Graph
Up: Global Alignment in linear
Previous: Global Alignment in linear
Itshack Pe`er
1999-01-03
, k*).
, m - k*).
, k*).
, m - k*).