Preface: Markov Models, CpG islands example

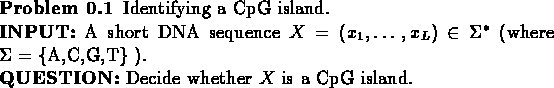
CpG is the pair of nucleotides C and G, appearing successively, in this order, along one DNA strand. It is known that due to biochemical considerations CpG is relatively rare in most DNA sequences. However, in particular sub-sequences, which are a few hundred to a few thousand nucleotides long, the couple CpG is more frequent. These sub-sequences, called CpG islands, are known to appear in biologically more significant parts of the genome. The ability to identify CpG islands along a chromosome will therefore help us spot its more significant regions of interest, such as the promoters or 'start' regions of many genes. We will start with the problem of identifying a given region as a CpG island, and then continue with the problem of locating CpG islands in a DNA sequence.

 

We can approach such problems using a Markov chain model. Let us denote for each $s,t \in \Sigma$ the transition probability:

$$a_{st} \equiv P(x_{i}=t \vert x_{i-1}=s)$$ (1)

We assume that $\{x_{i}\}$ is a random process with a memory of length 1, i.e., the value of the random variable x_i depends only on its predecessor x_i-1. Formally we can write:

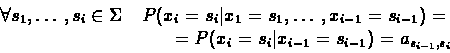$$\begin{split} \forall {s_{1},\ldots,s_{i} \in \Sigma} \quad ... ...}=s_{i} \vert x_{i-1}=s_{i-1}) = a_{s_{i-1},s_{i}} \end{split}$$ (2)

The probability of the whole sequence X will therefore be:

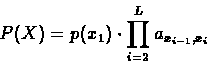$$P(X) = p(x_{1}) \cdot \prod_{i=2}^{L}a_{x_{i-1},x_{i}}$$ (3)

We can also add fictitious $begin \, (=x_{0})$ and $end \, (=x_{L+1})$ symbols to simplify the formula, where $\forall_{s \in \Sigma} \, a_{0,s} \equiv p(s)$ is the background probability of the symbol s. Hence:

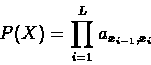$$P(X) = \prod_{i=1}^{L}a_{x_{i-1},x_{i}}$$ (4)

Let a⁺_st denote the transition probability of $s,t \in \Sigma$ inside a CpG island and let a^-_st denote the transition probability outside a CpG island (see table 6.1 for the values of these probabilities, taken from [4] ). We can compute a logarithmic likelihood score for the sequence X:

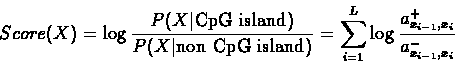$$Score(X) = \log \frac{P(X \vert \mbox{CpG island})}{P(X \vert... ...=1}^{L}\log\frac{a^{+}_{x_{i-1},x_{i}}}{a^{-}_{x_{i-1},x_{i}}}$$ (5)

The higher this score, the more likely it is that X is a CpG Island.

 

Table 6.1: Transition probabilities inside/outside a CpG island

+	A	C	G	T	-	A	C	G	T
A	0.180	0.274	0.426	0.120	A	0.300	0.205	0.285	0.210
C	0.171	0.368	0.274	0.188	C	0.322	0.298	0.078	0.302
G	0.161	0.339	0.375	0.125	G	0.248	0.246	0.298	0.208
T	0.079	0.355	0.384	0.182	T	0.177	0.239	0.292	0.292

 

 

A naive approach for solving this problem will be to extract a sliding window $X^{k}=(x_{k+1},\ldots,x_{k+\ell})$ of a given length $\ell$ (where $\ell \ll L$, usually several hundred bases long, and $1 \le k \le L-\ell$) to the sequence and calculate Score(X^k)for each one of the resulting sub-sequences. Sub-sequences that receive positive scores are potential CpG islands.

The main disadvantage in this algorithm is that we have no information about the lengths of the islands, while the algorithm suggested above assumes that those islands are at least $\ell$nucleotides long. Should we use a value of $\ell$ which is too large, the CpG islands would be short sub-strings of our windows, and the score we give those windows may not be high enough. On the other hand, windows that are too small might not provide enough information to determine whether their bases are distributed like those of an island or not. A better approach to such problems is described in the following section.