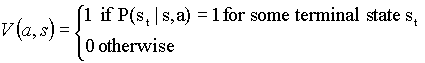Diminishing the Size of the Searched MDP
by Utilizing Symmetries
Introduction
The MAXQ Value Function Decomposition
A New State Abstraction
Formal Definitions
Results
Example: 2x2x2 Hungarian Cube
Summary
References
Introduction
This work is based on a paper by Thomas G. Dietterich [1]. This paper presents an approach to hierarchical reinforcement learning of fully observable MDPs, called the MAXQ value function decomposition.
Hierarchical reinforcement learning is a general name for several methods that try to diminish the searched policy space of the learning algorithm in a specific problem, by limiting the search to policies that follow certain constraints, that fit a hierarchical description of the problem in terms of sub-goals.
The MAXQ value function decomposition, is one such method. One of its advantages is that it allows the use of state abstractions, which enable ignoring certain aspects of a state when they are irrelevant. This work suggests a different kind of state abstraction not treated in the paper. The new state abstraction is intended to exploit symmetries that exist in a specific problem, and can diminish the size of the learned MDP by an order of magnitude and more.
A brief introduction of the relevant topics presented in Dietterich's paper follows. Afterwards, the new state abstraction will be described and defined formally, and results about its applicability will be shown. To demonstrate an application of the state abstraction, an example of its implementation on the problem of a Hungarian Cube will be given.
The MAXQ Value Function Decomposition
Dietterich presents an approach to hierarchical reinforcement learning, named the MAXQ value function decomposition. This approach is based on a programmer identifying sub-goals in the original problem’s MDP and defining subtasks that can achieve these goals.
This definition of sub-goals is then used to decompose the original problem’s MDP into sub-MDPs that are organized hierarchically – each sub-MDP’s actions can be both the primitive actions of the original MDP, or a non-primitive action, which is the execution of another sub-MDP. Each execution of a sub-MDP ends when a terminating state is reached.
Using this organization, the value function of the original MDP can be decomposed into an additive combination of the value functions of the sub-MDPs. The value function of any policy that is consistent with the given hierarchy can be represented using this method.
Dietterich presents an online model-free learning algorithm for the MAXQ hierarchy called MAXQ-Q, which converges with probability 1 to a recursively optimal policy. The recursively optimal policy is the policy in which every sub-MDP has the optimal policy when the sub-MDPs it can use as actions are executing their recursively optimal policies. This policy is not always the optimal hierarchical policy, since each sub-MDP learns its policy context-free of its parent MDPs. The paper considers two settings of rewarding the agent: episodic and discounted infinite horizon.
Some formal definitions and equalities used in the paper to describe the calculations of the MAXQ-Q algorithm are used later in this work:
Since a non-primitive action can take more that one step to execute, which can affect the reward in a discounted infinite horizon problem, the transition probability function incorporates the probability to complete the action a in a specific number of states: 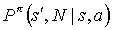 . The transition probabilities depend on the hierarchical policy
. The transition probabilities depend on the hierarchical policy  which is executed for the non-primitive actions.
which is executed for the non-primitive actions.
The completion function 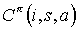 , is the expected discounted cumulative reward of completing subtask Mi after invoking the subroutines for subtask Ma in state s. The reward is discounted back to the point in time where a begins execution.
, is the expected discounted cumulative reward of completing subtask Mi after invoking the subroutines for subtask Ma in state s. The reward is discounted back to the point in time where a begins execution.
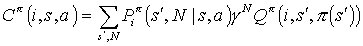
The projected value function for child task Mi in state s is then expressed thus:
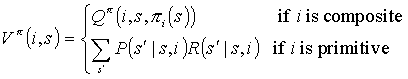 (1)
(1)
A new function defined for a MAXQ graph is the pseudo-reward function, 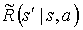 , This function allows the programmer to define different rewards for different terminating states of a sub-goal, without changing the original MDP.
, This function allows the programmer to define different rewards for different terminating states of a sub-goal, without changing the original MDP.
An important benefit of using the MAXQ method is that it allows the use of state abstractions. State abstractions are ways to let subtasks ignore large parts of the state space, and consequently diminish substantially the actual size of the problem to be solved by the MAXQ-Q algorithm. The paper presents five different conditions that allow introducing state abstractions without changing the convergence of the learning algorithm. Each condition can be applied independently of the others, and defines a set of states or of values stored by the algorithm, that can be ignored or merged. An example to such an abstraction is ignoring, within a certain subtask, some dimensions of the state, that are irrelevant for the subtask.
A New State Abstraction
This work suggests a new kind of state abstraction. The motivation is to exploit symmetries that exist in many problems, to diminish the state space that has to be searched by a learning algorithm. When several states in a problem are symmetric to each other, it will be shown that it is possible to find the optimal policy using only one representative state for each group of symmetrical states, where all these states together form a new, smaller MDP. This means that in a problem with several symmetries, the size of the MDP to be explored, can be a small fraction of the size of the original MDP.
Examples of symmetries can be found in many games. 2-dimensional and 3-dimensional Tic-Tac-Toe have spatial symmetry: a state of the game and its mirroring along any of the game board’s symmetry axes, can be treated as exactly the same state, with the exception that any action on the state should also be mirrored to give the same action for the mirrored state.
Another kind of symmetry that doesn’t involve axes of symmetry can be found in the maze problem presented by Parr [2] and referenced by Dietterich. The maze is presented in figure 1.
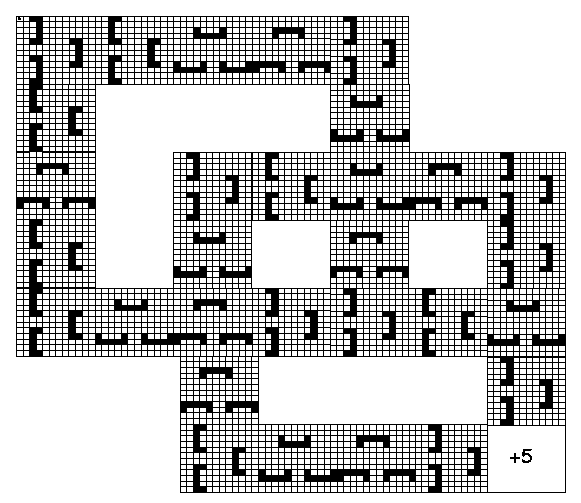
Figure 1 – Parr’s maze problem
In this problem, the agent starts in the upper left corner and has to reach the lower right corner. The obstacles on the way can only be detoured. Both Dietterich and Parr define the detouring of a single obstacle as a subtask that can be used by a parent task that moves from intersection to intersection. In these papers, there is no room for searching the best policy for detouring, since it is given with no degrees of freedom. But consider a problem in which the best policy to detour the obstacle is to be searched. Since all the obstacles have the same structure (with inner differentiation into obstacles with one open side and obstacles with two open sides), the best policy for detouring can be learned on all of them equally and simultaneously, if we ‘rotate’ the actions with the relative rotation of the obstacle.
The dramatic effect of using the symmetries of the problem can be demonstrated by the Hungarian Cube, where viewing different orientations and different color schemes of the cube as symmetric can give a diminishing of orders of magnitude in the number of states reachable from the starting state. This example will be described in more deail later in this work.
The following definitions formalize the concept of state symmetry, in a way that will enable learning the optimal policy for the original problem MDP, over a diminished MDP. The formalization and proofs will use the MAXQ value function decomposition and hierarchy for more generality, but they are, of course, also valid for a regular MDP, which can be viewed as a one-level hierarchy.
In this formalization, the symmetries will be used through two functions: T and L. T is a function from the set of states in the specific subtask into the same set of states. It maps each state to one of the states it is symmetric to (which can also be the state itself). For example, in a game with right-left symmetry, each state will be mapped either to itself or to its reflection along the symmetry axis. Usually, all the states that are symmetric to each other will be mapped to the same state, which is one of them chosen arbitrarily. L is a function that maps, for each state, a permutation over the actions. L is used to transform the actions in a state into the corresponding actions in the symmetric state it maps into by T. For example, if a state is mapped into its reflection, the permutation of actions for this state will transform each action into its reflection. This way, the result of an action performed on a state is symmetrical to the result of the transformation of the action defined by L, performed on the mapping of the state, defined by T.
To achieve the diminishing of the number of states, the set of representative states has to be a proper subset of the set of states within the subtask. Therefore, while this is not needed for the definitions and proofs, it is, in practice, the most important feature of the representation function.
Formal Definitions
Definition 1
Let Mi be a Max node in a MAXQ graph H for MDP M, Let Si be the set of states reachable in Mi, and Let Ai be the set of (primitive and non-primitive) actions possible in node i. A state correspondence for node i is an ordered pair (T, L), where T is a function 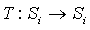 , and L is a function
, and L is a function 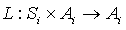 . In addition, for any
. In addition, for any 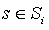 , the function
, the function 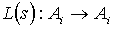 is one-to-one and onto.
is one-to-one and onto.
From now on, it will be assumed, for any state correspondence, that for all states 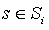 that are in the image of T when applied to Si, T(s)=s, and L(s)=Id. This assumption simplifies notation, and does not harm the generality of the arguments.
that are in the image of T when applied to Si, T(s)=s, and L(s)=Id. This assumption simplifies notation, and does not harm the generality of the arguments.
In reality, the state correspondence could be defined with 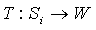 , where W is any set. Identifying W with Si was done here because in practice, the set W should usually be a subset of Si. This also simplifies the adaptation to the standard MAXQ-Q algorithm.
, where W is any set. Identifying W with Si was done here because in practice, the set W should usually be a subset of Si. This also simplifies the adaptation to the standard MAXQ-Q algorithm.
To simplify notation, the reverse function of 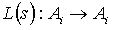 will be denoted by
will be denoted by 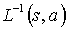 .
.
Definition 2
Let Mi be a Max node in a MAXQ graph H for MDP M, and let (T, L) be a state correspondence for node i. Two states 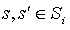 are equivalent under (T, L) if
are equivalent under (T, L) if 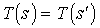 . This relation will be denoted by
. This relation will be denoted by 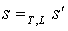 .
.
From the assumption pointed out above, it follows that for any 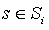 ,
, 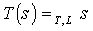 .
.
The equivalence relation defines a division of Si into equivalence classes. The size of the set of equivalence classes in Si, is |T(Si)|.
Definition 3
Let Mi be a Max node in a MAXQ graph H for MDP M, and let (T, L) be a state correspondence for node i. A policy 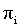 for node i is abstract with respect to (T, L) if for any pair of states
for node i is abstract with respect to (T, L) if for any pair of states 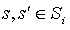 such that
such that 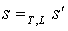 , the following equality holds:
, the following equality holds: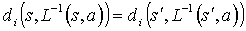 , where
, where 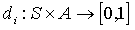 is the probability of
is the probability of 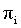 taking action a in state s.
taking action a in state s.
Definition 4
Let Mi be a Max node in a MAXQ graph H for MDP M. A state correspondence for node i (T, L), is a state symmetry for node i if the following properties hold:
- For each non-primitive child node j of node i, where Sj is the set of states reachable in Mj:
- the image of T when applied to Sj is a subset of Sj
- for any
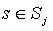 the image of L(s) when applied to Aj is one-to-one and onto Aj
the image of L(s) when applied to Aj is one-to-one and onto Aj
- The state correspondence (Tj, Lj) resulting from narrowing Ti to
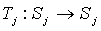 and Li to
and Li to 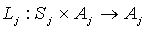 is a state symmetry for node j.
is a state symmetry for node j.
- For any stationary policy
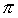 that is abstract with respect to (T, L), executed by the descendants of i, and for any pair of states
that is abstract with respect to (T, L), executed by the descendants of i, and for any pair of states 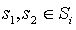 such that
such that 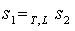 , the following equalities hold, for any action
, the following equalities hold, for any action 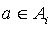 :
:
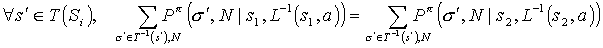 (2)
(2)
where T(Si) is the image of T when applied to Si, and 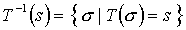 .
.
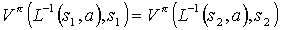
- For any pair of states
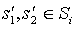 such that
such that 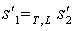 ,
,
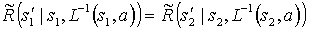
(4)
Obviously, any policy that is abstract with respect to a state symmetry (T, L) for some node i, is also abstract with respect to all the state symmetries of the descendants of node i, that result from narrowing the domains of T and L.
Results
Lemma 1
Let M be an MDP with a full-state MDP graph, and let (T, L) be a state symmetry for node i in a MAXQ graph H of M. Let 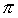 be a hierarchical policy that is abstract with respect to (T, L). Then the action-value function
be a hierarchical policy that is abstract with respect to (T, L). Then the action-value function 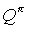 at node i, can be represented compactly, with only one value of the value function and the completion function for each equivalence class of states in Si. The action-value function can be computed as follows:
at node i, can be represented compactly, with only one value of the value function and the completion function for each equivalence class of states in Si. The action-value function can be computed as follows:

Proof:
Define a new MDP sym(Mi) at node i as follows:
- States: sym(Si) = T(Si) =
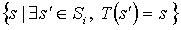
- Actions: Ai
- Transition probabilities:
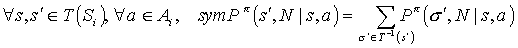
where 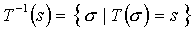 .
.
- Value function:
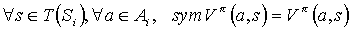
- Pseudo reward function:
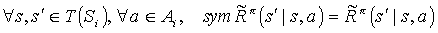
The policy  is well defined over sym(Mi), by considering its decisions for states in sym(Si) only.
is well defined over sym(Mi), by considering its decisions for states in sym(Si) only.
The action-value function for  over sym(Mi) is the unique solution to the following Bellman equation, for any
over sym(Mi) is the unique solution to the following Bellman equation, for any 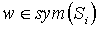 :
:
 (5)
(5)
The Bellman equation for the original MDP, Mi, for any 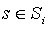 is:
is:
 (6)
(6)
Let w = T(s). Because (T,L) is a state symmetry for node i, we can use equation 3 and equation 4, and with the assumptions stated above for w, the following equalities hold:
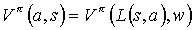
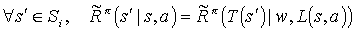
Using these, equation 6 becomes:

The summation over 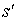 can be rearranged as a summation of summations over each equivalence class of states in Si to give:
can be rearranged as a summation of summations over each equivalence class of states in Si to give:
 (7)
(7)
We want to find the solution to the Bellman equations for the original MDP Mi, presented in equation 7, by referring to the solution for sym(Mi). Since the solution to the Bellman equations is unique, we only need to describe a set of values for 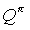 that solves the set of equations.
that solves the set of equations.
First, let us assume that for every 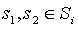 and
and 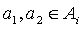 , such that
, such that 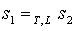 and
and 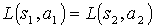 , the equality
, the equality 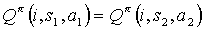 holds. It will be shown that the given solution is consistent with this assumption.
holds. It will be shown that the given solution is consistent with this assumption.
 is an abstract policy with respect to (T,L), therefore for any pair of states
is an abstract policy with respect to (T,L), therefore for any pair of states 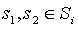 such that
such that 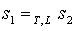 , the equality
, the equality 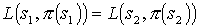 holds. Hence, following our assumption,
holds. Hence, following our assumption,  . We can now rewrite equation 7 to get:
. We can now rewrite equation 7 to get:

Since the bracketed expression does not depend on  , the order summation can be rearranged to give:
, the order summation can be rearranged to give:
 (8)
(8)
Rewriting equation 2 for w and s gives:

With this and with our definitions for sym(Mi), equation 8 becomes:
 (9)
(9)
Specifically, this equality is also true for s = w. Since L(w,a)=w, this gives the exact set of equations for  over T(Si) as the set of equations given by equation 5 for
over T(Si) as the set of equations given by equation 5 for  . Therefore, for every
. Therefore, for every 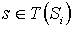 , and for every action
, and for every action 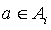 , we can let
, we can let 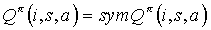 . In addition, for every
. In addition, for every 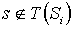 , the value of
, the value of 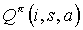 depends only on the value of
depends only on the value of 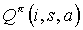 for
for 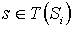 . Therefore equation 9 for
. Therefore equation 9 for 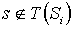 is a simple assignment. This completes the solution of the Bellman equations for Mi. Note that this solution does in fact follow our assumption: for every
is a simple assignment. This completes the solution of the Bellman equations for Mi. Note that this solution does in fact follow our assumption: for every 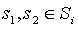 and
and 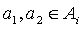 , such that
, such that 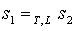 and
and 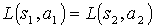 , equation 9 is exactly the same, therefore
, equation 9 is exactly the same, therefore 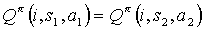 .
.
To conclude, we have shown the following relation between values of 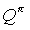 for node i:
for node i:
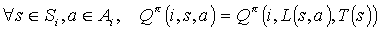
Which can be rewritten to give:
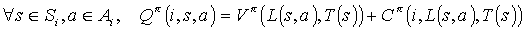 .
.
Q.E.D.
After having shown that any abstract policy can be represented compactly, we would like to know that the optimal policy at node i is also abstract with respect to (T,L).
Corollary 1
Consider the same conditions as Lemma 2, but with the change that the policy  that is abstract with respect to (T,L), is executed only by the descendants of node i, but not by node i. Let
that is abstract with respect to (T,L), is executed only by the descendants of node i, but not by node i. Let 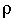 be an ordering over actions. Then the optimal policy
be an ordering over actions. Then the optimal policy 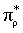 at node i, that breaks ties according to the ordering
at node i, that breaks ties according to the ordering 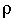 , is abstract with respect to (T,L), and its action-value function can be represented compactly as described in Lemma 1.
, is abstract with respect to (T,L), and its action-value function can be represented compactly as described in Lemma 1.
Proof:
The Bellman equations for the optimal action-value function is

where 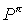 and
and 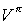 are the transition probability and value function when executing
are the transition probability and value function when executing  by the children of node i.
by the children of node i.
Define the policy 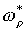 to be the optimal policy over the abstract MDP sym(Mi), and let
to be the optimal policy over the abstract MDP sym(Mi), and let 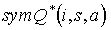 be the corresponding optimal action-value function. Then, by a similar argument to the one given in the proof of Lemma 2,
be the corresponding optimal action-value function. Then, by a similar argument to the one given in the proof of Lemma 2, 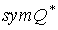 gives a solution to the optimal Bellman equation for the original MDP, Mi, by:
gives a solution to the optimal Bellman equation for the original MDP, Mi, by:
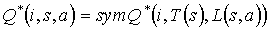
Therefore, the policy 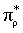 defined by
defined by  is an optimal ordered policy, and by construction, it is abstract with respect to (T,L).
is an optimal ordered policy, and by construction, it is abstract with respect to (T,L).
Q.E.D.
The above lemma and corollary show that we can save space by representing the completion function, value function and action-value function for only a subset of Si, which is the image of T, and use these values to find out the values for all the states in Si, either when evaluating a policy or when finding the optimal policy. The next corollary shows that we can not only save representation space, but also diminish the effective size of the MDP at node i, to the size of the image of T.
Corollary 2
Under the same conditions as Lemma 2, the MDP sym(Mi) can be simulated by running the original MDP Mi, and adding a simple interface defined by the functions T and L.
Proof:
To simulate sym(Mi) using Mi, the following interface will be added:
- Whenever the state of the MDP should be observed by the algorithm, instead of the true state of the MDP, s, the state that will be passed on to the observer will be T(S).
- Whenever the algorithm should perform an action on the MDP, instead of the action a passed by the algorithm, the action
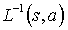 will be performed, where s is the current state of the MDP.
will be performed, where s is the current state of the MDP.
Let us now prove that the algorithm with this interface, learns the new MDP we defined in the proof to Lemma 1, sym(Mi).
- States:
The states seen by the algorithm are only states that are in the image of T when applied to Si, which is T(Si)=sym(Si).
- Actions:
The set of actions is the same as in the original MDP
- Transition probabilities:
For any state 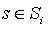 which is the current state of the MDP, an action
which is the current state of the MDP, an action 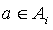 which is preformed by the algorithm, and the next state after performing the action
which is preformed by the algorithm, and the next state after performing the action 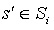 , the action actually performed is
, the action actually performed is 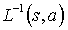 , therefore the transition probability is
, therefore the transition probability is 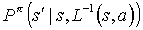 . In the simulated MDP, the current state is
. In the simulated MDP, the current state is 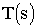 , the action is a, and the next state is
, the action is a, and the next state is 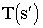 . The transition probability
. The transition probability 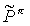 of the simulated MDP can be expressed using
of the simulated MDP can be expressed using 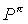 thus:
thus:

where the expectation is over the probability of each state to be the current state given that the observed current state is s. By equation 2 in the definition of state symmetry, the inner sum is equal for all the states in 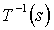 . Therefore we can represent
. Therefore we can represent 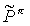 using only the transition probabilities from state s, for which L(s)=Id by our assumption:
using only the transition probabilities from state s, for which L(s)=Id by our assumption:

- Value function:
By equation 3 in the definition of state symmetry: 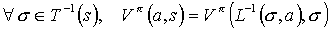
hence the value function is well defined for any state in the simulated MDP, as the value function in the observed state with the algorithm’s chosen action. This coincides with the definition of 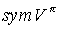
- Pseudo reward function:
By equation 4 in the definition of state symmetry:
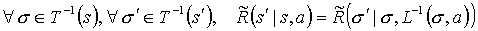
hence the pseudo reward function is well defined for any state in the simulated MDP, as the pseudo reward function in the current observed state to the next observed state, with the chosen action a. This coincides with the definition of 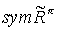 .
.
We have shown that the algorithm, using the described interface, runs over a simulation of sym(Mi).
Q.E.D.
Example: 2x2x2 Hungarian Cube
In this section, the example of a 2x2x2 Hungarian Cube will be used to demonstrate the application of the definition of a state symmetry. This simplification of the 3x3x3 Cube, is taken to shorten the description, but the definitions can be easily extended to fit the full cube.
The goal is to find, for a specific start state, the shortest path to a terminating state: this state can be any of the configurations in which, on every face of the cube all the squares are the same color. Therefore, the reward scheme will be discounted infinite horizon, with a reward of 1 for reaching a terminal state.
The number of different configurations reachable from the starting state in the 2x2x2 Cube is 8!*38/(3*2) = 44089920 [3]. Each configuration can be represented by the color of each square out of the 24 squares of the face of the cube. The order of the squares in the representation can be arbitrarily chosen. From now on, this order will be used to describe the different squares in a state.
The possible actions on the cube are rotating one of the halves of the cube along its center pivot clockwise or counter-clockwise. This gives 12 different possible actions. The actions can be represented by the rotation axis, the half to be moved, and the direction of rotation - clockwise/counter-clockwise.
The state symmetry that will be defined exploits both the spatial symmetry and the symmetry between the different colors.
First, we will define an ordering over the states, that does not differentiate states that are different only in their color assignments.
To compare two states, first their representation will be converted into the same color scheme: For each state, the color of the first square will be replaced by an arbitrary color ‘1’. The next color found when going over the squares in order, will be replaces by a color ‘2’, and so forth.
Second, the new representation will be compared using a lexicographic comparison: The first different ‘color’ square will determine which of the states is bigger. If, in the new color scheme, both states are exactly the same, they are equal.
Now, we can define the state symmetry:
For finding T(s), we will compute the minimal state, s', in the set of states that can be reached by a composition of any subset of the following transformations on s:
- Mirroring the Cube’s X axis
- Mirroring the Cube’s Y axis
- Mirroring the Cube’s Z axis
- Permuting the x axis and the y axis
- Permuting the y axis and the z axis
- Permuting the z axis and the x axis
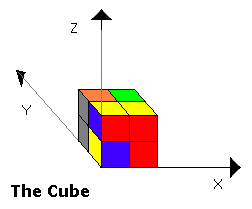
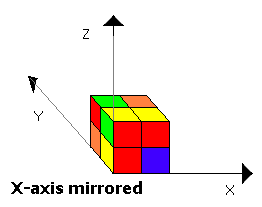
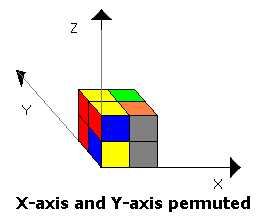
The number of possibilities that must be tested here is 48, some of which might give the same configuration.
The color scheme of s' will be changed using the method described above, and the result will be defined to be T(s).
L(s,a) will be defined using the computation of T(s): The transformation over the actions for state s will be the same of transformations that gave the chosen state s', when applied to the actions.
The following table gives, for every transformation defined above, the corresponding transformation for the actions.
|
Transformation for T(s) |
Transformation for L(s) |
|
Mirroring X axis |
For a=(X-axis, half, direction), the half and direction are to be inverted |
|
Mirroring Y axis |
For a=(Y-axis, half, direction), the half and direction are to be inverted |
|
Mirroring Z axis |
For a=(Z-axis, half, direction), the half and direction are to be inverted |
|
Permuting the x axis and the y axis |
Inverse the direction of rotation for any a. For a = (X-axis, half, rotation), and for a = (Y-axis, half, rotation), replace X-axis by Y-axis and vice versa. |
|
Permuting the y axis and the z axis |
Inverse the direction of rotation for any a. For a = (Y-axis, half, rotation), and for a = (Z-axis, half, rotation), replace Y-axis by Z-axis and vice versa. |
|
Permuting the z axis and the x axis |
Inverse the direction of rotation for any a. For a = (Z-axis, half, rotation), and for a = (X-axis, half, rotation), replace Z-axis by X-axis and vice versa. |
Let us now see that this indeed defines a state symmetry:
First, all the functions over A are clearly permutations, therefore (T,L) is a state correspondence.
Second, let us examine the conditions in definition 4:
Condition (1) is trivially satisfied, since this problem has no MAXQ hierarchies.
For condition (2.1), we need to show that for any pair of states 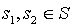 such that
such that 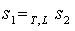 , and for any action
, and for any action 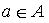 :
:
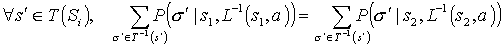 .
.
Note that, since in this problem the action results are deterministic, it is enough to show that if the action 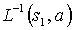 takes s1 to
takes s1 to 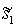 , and the action
, and the action 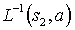 takes s2 to
takes s2 to 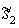 , then
, then 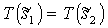 .
.
It can be seen from the definition of T and L, that whenever s1 and s2 are symmetric, the corresponding action defined by 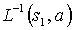 and
and 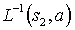 takes the pair of states into two states that are also symmetric. By the definition of T, all the states that are symmetric to each other, are taken by T to the same state, because T always chooses the orientation that gives the minimal state out of all the possible symmetric configurations, and always gives the same color scheme. Therefore,
takes the pair of states into two states that are also symmetric. By the definition of T, all the states that are symmetric to each other, are taken by T to the same state, because T always chooses the orientation that gives the minimal state out of all the possible symmetric configurations, and always gives the same color scheme. Therefore, 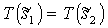 .
.
For condition (2.2), we need to show that that for any pair of states 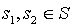 such that
such that 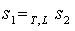 , for any action
, for any action 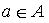 :
: 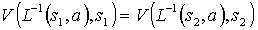 . Using the definition of the value function in equation 1, since the action is always primitive, and since the reward in this problem is independent of the starting state and of the action, we get:
. Using the definition of the value function in equation 1, since the action is always primitive, and since the reward in this problem is independent of the starting state and of the action, we get:
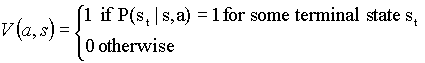
Therefore, by the same argument made for condition 2.1, and since the terminating states form an equivalence class with respect to (T,L), the equality holds.
Condition 2.3 is trivially satisfied, since we have no pseudo-reward in this problem.
We have shown that (T,L) is a state symmetry. This symmetry can be used to implement an interface to a learning agent as described in the proof to corollary 2. The size of the biggest equivalence class of the states in the original MDP is the number of different reachable orientations x the number of different reachable color schemes = 720. (The equivalence class is smaller for states that are symmetric to themselves). The size of the searched MDP can, therefore, be dimminished substantially.
Summary
This work shows that in a problem that has inner symmetries, these can be exploited to boost the learning algorithm, using an interface between the learning agent and the environment. The discovery and formalization of the symmetries in a specific problem have to be made by hand. Nonetheless, in some problems this effort can turn an unsolvable problem into a solvable one. With more work on this subject, it is probable that the state symmetries of groups of problems with similar structure can be defined in general terms with few free parameters. An example of such a group of similar problems is the group of problems with the planar or spatial symmetry of a square or a cube.
References
[1] Thomas G. Dietterich, (1999). Hierarchical Reinforcement Learning with the MAXQ Value Function Decomposition. Technical Report, Department of Computer Science Oregon State University, Corvallis, Oregon.
[2] Parr, R. & Russel, S. (1998). Reinforcement Learning with Hierarchies of Machines. Computer Science Division, UC Berkley.
[3] Hofstadter, D.R. (1985). Metamagical Themas: Questing the Essence of Mind and Pattern. pages 301 - 366. Published by Basic Books, New York
![]() . The transition probabilities depend on the hierarchical policy
. The transition probabilities depend on the hierarchical policy ![]() which is executed for the non-primitive actions.
which is executed for the non-primitive actions.
![]() , is the expected discounted cumulative reward of completing subtask Mi after invoking the subroutines for subtask Ma in state s. The reward is discounted back to the point in time where a begins execution.
, is the expected discounted cumulative reward of completing subtask Mi after invoking the subroutines for subtask Ma in state s. The reward is discounted back to the point in time where a begins execution.
![]()
![]() , This function allows the programmer to define different rewards for different terminating states of a sub-goal, without changing the original MDP.
, This function allows the programmer to define different rewards for different terminating states of a sub-goal, without changing the original MDP.
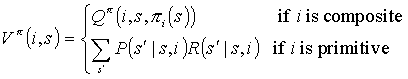 (1)
(1)
 (5)
(5) (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)