
This work was submitted as a final project in a Reinforcement Learning course given in Tel Aviv University, in Autumn 1999/2000, by Prof. Yishai Mansour. The work compares several methods to automatically play a reduced version of the Tetris game. We shall describe a few Reinforcement Learning (RL) methods that we have examined, and will compare their performance with those of a non-learning simple algorithm, as well as with previous work in RL performed to solve the same problem (by Stan Melax). The main results of our experiments are presented, as well as the code in use.
The problem being dealt with is a reduced version of the Tetris game. The Tetris game has several characteristics making it an interesting problem for the field of RL. A complete representation of the problem includes huge number of states making a definition of a non-learning strategy practically impossible. The problem is an online one, forced to take decisions without having the entire input available. The specific reduction of the game chosen was based on two main reasons. The first was to cope with a problem in a size allowing to compare various RL methods without involving additional tools such as Neural Networks (NN). Thus being able to concentrate on the various methods themselves and their preferred parameters. The second reason was the previous work done on the subject. Choosing the same definition enables comparison of the performance of the various methods, both in absolute terms and in terms of convergence rate.
Tetris is an exciting action game. Throughout the game, Tetris pieces fall from the top to the bottom of the playing area. When the Tetris pieces form a solid row of blocks across the playing area, that row vanishes. Because this is the only way to remove blocks, the user should try to form solid rows whenever possible. The game ends when the pieces stack up to the top of the playing area. One can manipulate a piece only when it is falling. Falling pieces may be rotated, moved horizontally, or dropped to the bottom of the playing area. The dimensions of the playing area are width of 10 columns and height of 25 rows. There are 7 different playing pieces all consist of exactly four blocks (the name of the original game was derived from the Latin word to 'four').
The reduced version investigated in this work was limited to six columns. The height of the playing area is unlimited since this limitation is only relevant for human players who are influenced by the reduced time constraint when the blocks pile up. Another deviation from the original game is the group of pieces in use. Following Melax the pieces are:
figure 2: playing pieces
During the simulation, complete rows are indeed removed. The game is limited by the number of pieces thrown, and the criterion used at the end of each game to the performance of a give strategy is the height of the pile (actually the highest column piled).
The first strategy used to decrease the size of the state space was to merely describe the upper contour of the game blocks (the sky line). This is a compact representation that still holds most of the significant information needed by the user to make his move. Two versions of the contour representation were examined. Version one treated any difference between neighboring columns as if it was either 1 or (-1). A more sophisticated version allowed each difference to take the values of {-2, -1, 0, 1, 2}. This description holds all the information required to place one piece in the best fitting place disregarding extreme non-balanced situations (which are fairly rare). The representation also looses information regarding holes in deeper levels. The first version consists of 243 (=3^(6-1)) states, while the second version requires 3125 different states.
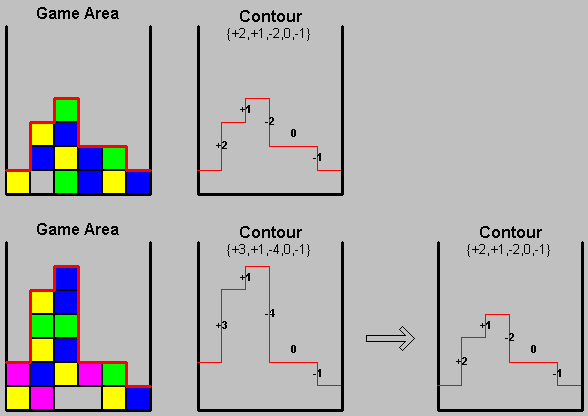
figure 3: bounding contour
The second approach was to refer to the Top Two Levels (TTL) of the game. Defining M as the height of the highest column, this representation holds the information regarding rows number M-1 and M. In the reduced version of the game, this technique requires 4096 (=2^12) states. Though this representation does not hold information regarding rows, two and three levels from the top, it does include information regarding holes located one level from the surface. This approach was initially used by Melax.
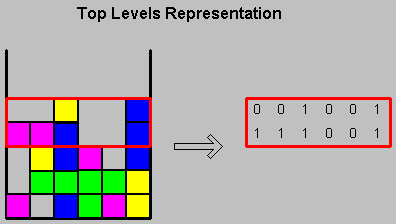
figure 4: top level representation (TTL)
Using both representation a couple of RL techniques were examined; the Q-learning, the SARSA, and the direct use of TD(0) as used in previous work. In all the techniques various parameters had to be considered. The learning ratio, represented by Alpha, and the discount factor, represented by Lambda. For Alpha, there could be a choice of a constant, which was suggested by Melax, or a decreasing value proportional to 1/n, as suggested in the RL literature, and assuring convergence. In addition, the relation between exploration and exploitation while learning had to be determined. The realization of this relation during learning is in the ratio between using random policy to using a predefined policy (or a greedy one in the case of SARSA).
The performance of all the above were compared against the work of Melax, as well as to the performance of a greedy static strategy, minimizing the center of gravity of the next piece.
The second representation, referred as TTL, achieved better performance using all strategies. We therefore decided to take it one step forward and by reducing its state space, make it more accurate and enable the research of its parameters. The reduction of the state space was done using symmetry. There were 64 (=2^6) symmetric states, while all the rest 4032 were asymmetric and thus each mirror couple could be represented by a single state. The various pieces' location and rotation could be simulated by the same pieces, located in mirrored location and using different rotation. Altogether this approach included 2080 (=(4096-64)/2+64) states. The effort in this direction was based on the fact that the negative effect on the learning rate when increasing the state space is of high order. Therefore, we expected a significant acceleration in the learning rate if a reduction in the space state could be made. This approach has proved itself beyond any expectation.
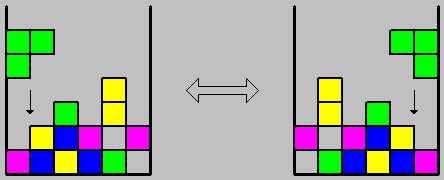
figure 5: applying symmetry
The exact definition of the game was based on Melax, to enable performance comparison. Each game, therefore, consisted of 10k pieces, uniformly chosen from the five possible pieces. The performance of an algorithm was measured according to the height of the highest column left after the 10k pieces were dropped, and after full rows were removed.
The benchmark application included two main modules; one implemented the algorithm, either RL based, or a static one, while the other was a full simulation of the game, enabling to track the precise game state, deriving the next state for RL purposes, and quoting the final results correctly.
Many configurations were tested according to the following approach. First the convergence was tested. This was done by recording 1024 games and analyzing the behaviour of their average, variance and resemblance to Melax' results (~240), which were estimated at the time as good ones. Analyzing the variance also implied about the stability of the solution. Configurations that fail to converge, or to reach reasonable results, were dropped at early stages. Others went through some deeper analysis and parameter calibration. The results are presented as height of the highest column, for each power-of-two (1, 2, 4, . . . 256) game.
We will now review and analyze the results of four configurations, which seemed to pass the first filter of convergence and average performance.
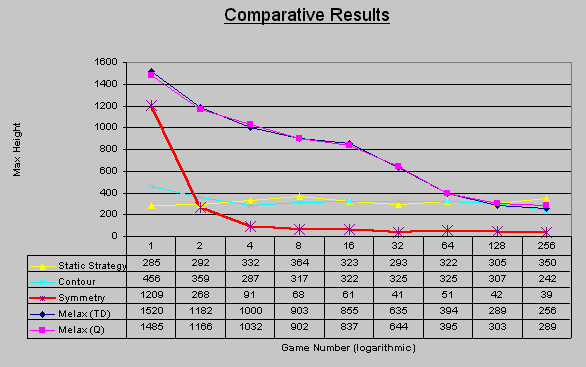
figure 6: learning rate of selected configurations
The first two configurations tested were using the TTL representation with Q-learning and with TD learning (Melax). These two had very similar performance, with a marginal advantage to the Q-learning. Both configurations seemed to be close to convergence, however, they both were not very stable when following consecutive games. We referred to the given parameters in use as optimal and compared the rest of our work to the results of these two configurations. These two configurations used constant values of Alpha, which could not be substituted by a decreasing function without a significant degradation of the results. The results of the later experiments implied why. The system was still far from convergence.
Next, a greedy static strategy was examined as a reference. This strategy, naturally, did not show any tendency to improve. However, it served both as a reference to the absolute results, and to the expected variance between consecutive games, caused by the random nature of the game pieces.
The experiments using the contour representations gave results which were quite close to the results given by Melax. The Q-learning version required an intelligent offline policy in order to give any results that seem to converge anywhere. The offline policy used was the one described above. Some exploration was added to the offline policy, to increase the chance of visiting rare states. Two types of explorations were examined. The first was to play a random game once in every n games. The second was to take a random action once in every n shapes. The second approach was found to be more successful and the results presented are using this approach. In both methods the exploration did not helped to reach all the rare states often enough for correct updates of the Q-learning table values. The common states were not visited enough times as well, thus preventing convergence in a reasonable time. The rare states not visited enough caused abnormal behaviour viewed by a game area extremely unbalanced.
The contour representation was tested using the Sarsa algorithm as well. The performance was very similar to the performance of the Q-learning. An intelligent initialization was needed in order to get reasonable results. The Sarsa's table was initialized using the static policy that was described above. No real improvement over this initialization was observed.
The last configuration tested was the symmetry based TTL with the reduced state space. The results for this configuration outperformed in any parameter all the other configurations. In addition, even without comparison to other configurations, the results themselves proved convergence and stability. The learning rate was very fast, and the variance later on (after 25 games) was very low (relating to the absolute values). This configuration used a value of Alpha, decreasing as a function of 1/n, thus assuring continuous convergence.
The conclusions derived from this work deal with the size of the state space and with the behaviour of the parameters Alpha and Lambda.
The size of the state space was proved to have the highest influence on the system learning time, by far. It makes the relevancy of other factors such as complexity of each state, or calculation of a single action, completely insignificant. A related conclusion is that it is worth giving up some precision in the system description, thus achieving a smaller state space, enabling the learning mechanism to converge, than to have a more detailed system which will only be sub optimal. Considering the minimal information in use through this work, it can be concluded that, at least for this problem and its alike, most of the relevant information resides on the surface. Any deeper information, not only reduces the chances of the learning system to converge, but its contribution to the system is marginal.
The above also agrees with the relative low Lambda found to be useful. This low value suggests that the connection between neighboring states is much lower, than one might guess. In other words, much less importance should be given to future actions than to current reward, in this problem.
The first conclusion regarding the learning parameters, is that while the state space is not small enough, the calibration of the parameters is merely black magic. The parameters do not take their theoretical role, and finding their optimal values is more a matter of chance or exhaustive search than operating theoretical considerations.
After having a small enough representation of the system, we could easily calibrate the parameters to the preferred learning and convergence ratio, based on the RL theory. The sparse relation between neighboring states led to relatively low Lambda, and an Alpha with the behaviour of 1/n led to convergence, as expected.
For this problem, RL solutions, when employed correctly, outperformed a static greedy algorithm, based on similar information. The conclusion may be that in such problems, with a huge state space, our first intuition in choosing the basic rules for an algorithm might be misleading, while RL mechanisms might concentrate to a set of rules with better performance.
This work dealt with a reduced version of the Tetris game for various reasons. However, the conclusions of this work regarding the required state space and the irrelevancy of a detailed state description, imply that a good working solution for the full version of the classic 2D Tetris game might be explored, as well as the 3D version. When the reviewed tools are not enough, stronger compaction tools might be required such as Neural Networks, to compactly represent the state space.
Other extensions of the game that are available to human users and might be interesting to cope with using RL tools. Among which are the limited working height, and the information regarding the next piece to appear.
| Yael Bdolah | yael@artcomp.com |
| Dror Livnat | livnat@math.tau.ac.il |
Last updated: March 20, 2000.