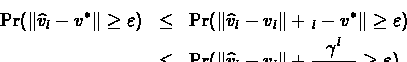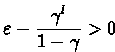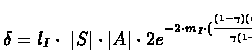Next: Conclusions
Up: Proof for The Indirect
Previous: Notations
Bounding the Number of Calls to PS(M)
We've seen:
For every
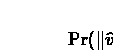 ,
,
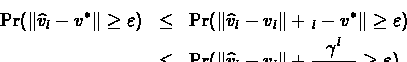 |
(22) |
Let's find mI and lI such that
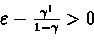 |
(23) |
By the previous claims, it suffices to find mI and lI s.t.:
- 1.
-
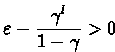
- 2.
-
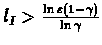
Note that
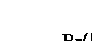 (since
(since
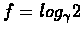 ). Then we can
set (taking upper value if necessary):
). Then we can
set (taking upper value if necessary):
The number of calls to PS(M) is mI:
Here, again, mI and lI must be natural numbers, but taking
their upper value won't change the asymptotic complexity, so, the
number of calls to PS(M) by the indirect algorithm is:
Yishay Mansour
2000-05-30
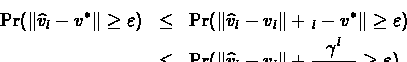
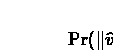 ,
,