


Next: Algorithm
Up: TD( ) algorithm
Previous: TD( ) as generalization
Forward Updates Versus Backward Updates
In all definitions of
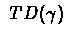 we looks on updates
occurring in forward direction in time (looking to the "future")
like in MC method. We want to define scheme for online updates and
so we need to find the way to look on updates in backward
direction ("past"). We like that at the end of the run, updates
would be the same for both schemes.
we looks on updates
occurring in forward direction in time (looking to the "future")
like in MC method. We want to define scheme for online updates and
so we need to find the way to look on updates in backward
direction ("past"). We like that at the end of the run, updates
would be the same for both schemes.
For implementation of such method, an additional variable which
holds weight of a state in a run will be provided for every run.
Every step we multiply all those variables (called eligibility
trace) by
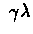 and for current state we add 1.
Formally,
and for current state we add 1.
Formally,
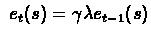 if
if
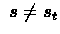
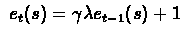 if
if
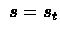
Every time we visit a state , its weight is going up and for
states not visited theirs weight is going down. Let us define:
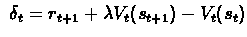 .
.
Now the update would be,
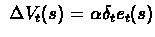 .
.
Yishay Mansour
2000-01-06