Convergence

According to the Law of Large Numbers the average converges to the expected value :

$\hat{V_{n}}\longrightarrow \bar{v}=E[V_{i}]$, note that clearly
$E[\hat{V_{n}}]=\bar{v}$.

The variance is :

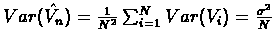$Var(\hat{V_{n}})=\frac{1}{N^{2}}\sum_{i=1}^{N}Var(V_{i})=\frac{\sigma^{2}}{N}$, where
$\sigma^{2}=Var(V_{i})$.

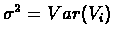This implies that when N goes to infinity we have,

$\lim_{N \rightarrow \infty}\frac{\sigma^{2}}{N}=0$

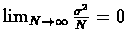
so as the sample size increases, the difference between the average and the expected value decreases.