Example

Next: About this document ... Up: Evaluating Policy Reward Previous: Every Visit

Example

Figure: Example Diagram
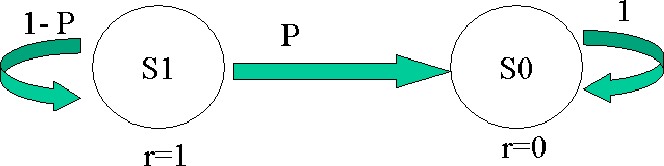
$\begin{figure}\psfig{file=figure1.ps,width=6in,clip=} \end{figure}$

Consider the MDP in the Figure 7.1. Let N be the length of the run. We choose $\gamma = 1$ (undiscounted). It is easy to see that,

$V^{\pi}(s_{1}) = \frac{1}{p} = E[N]$ ,

since the distribution is geometric ("success" with probability p when moving to s₀). However note that $r(s_{1},T,j) \geq r(s_{1},T,j+1)$ , which implies that r(s₁,T,j) are independent.
The return from the k-th appearance of S₁ until the end of the run is N-k (there are N steps in the run, each of them with reward 1 and the run ends the first time we get to S₀).
The average is $\frac{1}{N} \sum_{k=0}^{N-1}(N-k) = \frac{1}{N}\frac{N(N+1)}{2} = \frac{N+1}{2}$
Hence $E[\frac{N+1}{2}]=\frac{\frac{1}{p}+1}{2}=\frac{1+p}{2p}$ .
Note that this is different from $E[V^{\pi}(s_{1})]=\frac{1}{p}$ .
The difference (bias) is because the random variables are dependent.

Error Calculations

The fact that Every Visit is biased does not implies that it is inferier to First Visit , as an estimate. Consider using a single run to estimate the return in the above example.

First Visit :

$Var(\hat{V_{F}}(S_{1}))=E[N^{2}]-E^{2}[N]=\frac{1}{p^{2}}-\frac{1}{p}$

Note that the variance in this case can be bigger than the expected value when p is small. for example if p=0.1 then the expected value is 10 and variance is 90.
Every Visit :

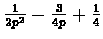
$E[(\frac{N+1}{2}-\frac{1}{p})^{2}]=$ $\frac{1}{2p^{2}}-\frac{3}{4p}+\frac{1}{4}$
For each p<1, the expected square error in Every Visit is smaller than in First Visit , meaning that Every Visit creates a biased estimation but it's variance is much smaller. The reason is that Every Visit contains many more samples. Note that in Every Visit the average is computed on all the runs, and not within the runs.

Next: About this document ... Up: Evaluating Policy Reward Previous: Every Visit
Yishay Mansour
1999-12-16