


Next: Example: Running Policy Iteration
Up: Policy Iteration
Previous: Policy Iteration Algorithm
Convergence of Policy Iteration Algorithm
We shall
see that when the number of states - |S|, and the number of
actions - |A| are finite, there are no two
non-consecutive iterations with the same policy, unless we have an optimal policy.
Therefore dn converges to the optimal policy
in a finite number of
steps. The key to the convergence of dn is the monotonicity of 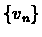 .
.
Claim 6.4
Let
vn,
vn+1 be the values of consecutive iterations of the above
algorithm, then
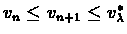
.
Proof:Let dn+1 be the policy in the policy improvement step, then
Therefore:
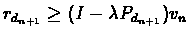 .
Multiplying by
.
Multiplying by
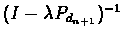 we get:
we get:

Note: The above claim is valid even when S or A are infinite.
Theorem 6.5
Let
S and
A be finite,
then the
Policy Iteration algorithm converges to the optimal
policy after at most |
A|
|S| iterations.
Proof:Clearly,
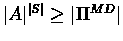 .
According to claim
.
According to claim ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) , in each step
, in each step
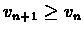 except for the
last step in which
vn+1 = vn. Therefore no policy
except for the
last step in which
vn+1 = vn. Therefore no policy
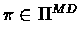 can appear in two different iterations. Hence the number
of iterations
can appear in two different iterations. Hence the number
of iterations
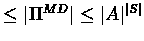




Next: Example: Running Policy Iteration
Up: Policy Iteration
Previous: Policy Iteration Algorithm
Yishay Mansour
1999-12-18
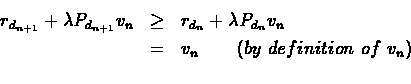
![]() .
According to claim
.
According to claim ![]() , in each step
, in each step
![]() except for the
last step in which
vn+1 = vn. Therefore no policy
except for the
last step in which
vn+1 = vn. Therefore no policy
![]() can appear in two different iterations. Hence the number
of iterations
can appear in two different iterations. Hence the number
of iterations
![]()
![]()