


Next: Example: Running Value Iteration
Up: Finding the Optimal Policy:
Previous: Correctness of Value Iteration
Convergence of Value Iteration Algorithm
In this
section we show that the convergence to the optimal policy of VI
algorithm is monotonic, and that the convergence is exponentially
fast in the parameter 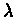 .
.
Proof:For part (1), let
Since
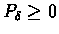 ,
it follows that
,
it follows that
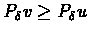 .
Therefore:
.
Therefore:
This proves part (1).
From part (1) it follows by induction
that if 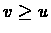 ,
then
,
then
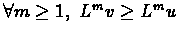 .
.
To prove part (2):
 the above claim it follows that if
the above claim it follows that if
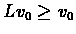 (or
(or
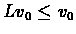 ), VI will converge
monotonically, which
means that running more iterations will always lead to a better policy. If all rewards in a
specific MDP are non-negative (or non-positive), we can choose
), VI will converge
monotonically, which
means that running more iterations will always lead to a better policy. If all rewards in a
specific MDP are non-negative (or non-positive), we can choose
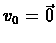 ,
which assures
the condition is
met.
,
which assures
the condition is
met.
Theorem 6.3
Let
vn be the sequence of values computed by the VI
algorithm.
- 1.
-
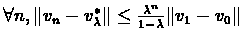
- 2.
-
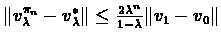 ,
where
,
where 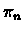 is the policy that is defined by vn.
is the policy that is defined by vn.
Proof:Part (1): We will use the result of part (![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) ) in theorem
) in theorem ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) :
:
To use it we bound:
Let
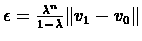 ,
so that we can use theorem
,
so that we can use theorem ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) to conclude that:
to conclude that:
Which proves part (1).
To prove part (2) we bound:
The following bounds derive (a) from the same result of
theorem ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) and (b) from part (1) of this
theorem, respectively:
and (b) from part (1) of this
theorem, respectively:
The last inequality follows form L being a contracting operator, thus ending the proof of part
(2)
From this theorem it follows that each iteration of the
VI algorithm is closer to
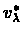 by a factor of
by a factor of
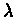 .
As
.
As 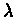 approaches 1, the rate of convergence
decreases. The bounds we have shown can be used to determine the number of iterations needed for
a specific problem.
approaches 1, the rate of convergence
decreases. The bounds we have shown can be used to determine the number of iterations needed for
a specific problem.



Next: Example: Running Value Iteration
Up: Finding the Optimal Policy:
Previous: Correctness of Value Iteration
Yishay Mansour
1999-12-18
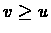 then
then
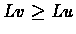
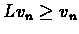 then
then
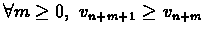
![]() ) in theorem
) in theorem ![]() :
:
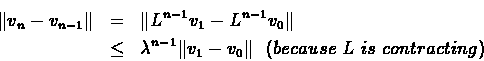
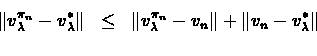
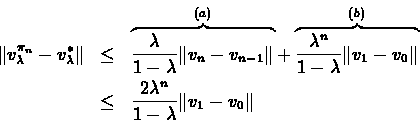
![]() by a factor of
by a factor of
![]() .
As
.
As ![]() approaches 1, the rate of convergence
decreases. The bounds we have shown can be used to determine the number of iterations needed for
a specific problem.
approaches 1, the rate of convergence
decreases. The bounds we have shown can be used to determine the number of iterations needed for
a specific problem.