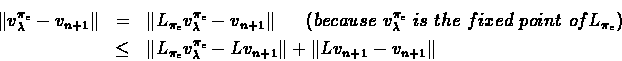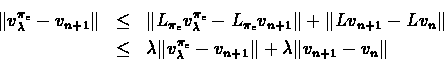Next: Convergence of Value Iteration
Up: Finding the Optimal Policy:
Previous: The Value Iteration Algorithm
Correctness of Value Iteration Algorithm
In the following theorem we show that the algorithm finds an 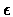 -optimal policy in a
finite number of steps. Note that the selected policy might in fact be the optimal policy, but
we have no way of knowing that in advance.
-optimal policy in a
finite number of steps. Note that the selected policy might in fact be the optimal policy, but
we have no way of knowing that in advance.
Proof:Parts (1) and (2) follow directly from the properties of the
series
vn+1 = Lvn, that were shown in Lecture 5.
For
part (3) we assume that
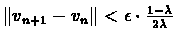 ,
as is the case when the algorithm
stops, and show that
,
as is the case when the algorithm
stops, and show that
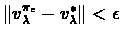 ,
which would make the policy
,
which would make the policy
 -optimal.
-optimal.
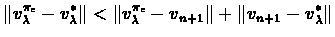 |
|
|
(6.1) |
We now bound each part of the sum individually:
Since
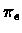 is maximal over the actions using
vn+1, it implies that
is maximal over the actions using
vn+1, it implies that
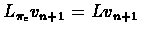 and we conclude that:
and we conclude that:
From the inequality it follows:
For the second part of the sum we derive similarly that:
From which part (4) of the theorem also follows.
Returning to
inequality ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) , it follows:
, it follows:
Therefore the selected policy
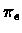 is
is
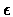 -optimal.
-optimal.



Next: Convergence of Value Iteration
Up: Finding the Optimal Policy:
Previous: The Value Iteration Algorithm
Yishay Mansour
1999-12-18
![]() ,
as is the case when the algorithm
stops, and show that
,
as is the case when the algorithm
stops, and show that
![]() ,
which would make the policy
,
which would make the policy
![]()
![]() -optimal.
-optimal.