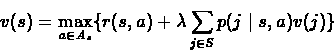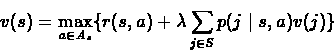Next: The Value Iteration Algorithm
Up: No Title
Previous: No Title
Finding the Optimal Policy: Value Iteration
In this
section we present the Value Iteration algorithm (also referred to
as VI) for computing an 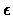 -optimal policy6.1 for a discounted infinite horizon problem.
-optimal policy6.1 for a discounted infinite horizon problem.
In Lecture 5 we showed that the Optimality Equations
for discounted infinite horizon problems are:
We also defined the non-linear operator L:
For which it was shown, that for any starting point
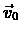 ,
the series
,
the series
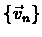 defined by
defined by
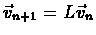 ,
converges to the optimal return
value
,
converges to the optimal return
value
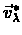 .
.
The idea of VI is to use these
results to compute a solution of the Optimality Equations. The VI
algorithm finds a Markovian stationary policy that is
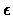 -optimal.
-optimal.
Yishay Mansour
1999-12-18