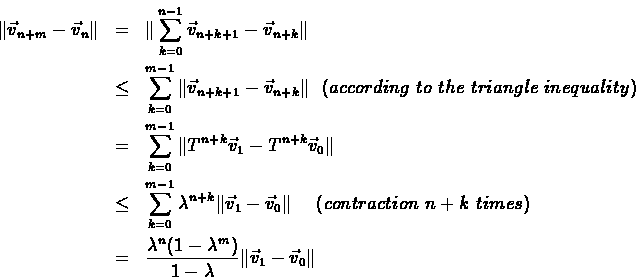Next: is a fixed point
Up: The Solution of the
Previous: The Solution of the
Existence of a
limit 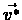
Since the coefficient decreases as n increases,
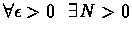 such that
such that
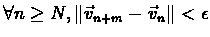
Thus the series 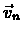 has a limit.
has a limit.
Let us
call this limit 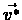 and show that
and show that 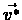 is a fixed
point of the operator T.
is a fixed
point of the operator T.
Yishay Mansour
1999-11-24