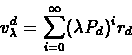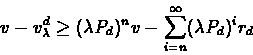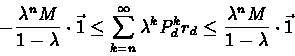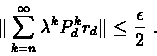Next: The Solution of the
Up: Computing the Optimal Policy
Previous: Computing the Optimal Policy
Optimality Equations
For a finite horizon we gave the following equations:
For a discounted infinite horizon we have similar equations. We
will show that the Optimality equations are:
First we show that maximizing over deterministic and stochastic
policies yield the same value.
Proof:
Since
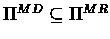 ,
the right side of the
equality is at least as large as the left.
,
the right side of the
equality is at least as large as the left.
Now we show that the
left side is at least as large as the right.
For
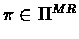 and v we define
and v we define
Fix a state 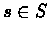 .
The value of
.
The value of  is a weighted average of
ws(a), and we have
is a weighted average of
ws(a), and we have
Hence
For any
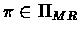 .
.
This shows that the left hand side
in the theorem is at least as large as the right hand side, which
completes the proof.

Let us define the non-linear operator L:
Therefore we can state the optimality equation by
It still remains to be shown that these indeed are optimality
equations, and that the fixed point of the operator is the optimal
return value.
Proof:We start by proving (1)
this implies that for any policy d,
For a given policy d
By subtraction
Since
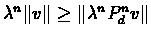 and
and
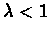 ,
we have that for any
,
we have that for any
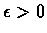 there exists an N > 0, such that for all n > N we have
there exists an N > 0, such that for all n > N we have
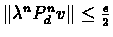
Since
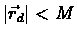 we can write:
we can write:
For a large enough n we have
By this we derive that
and for all d
Thus
As this is true
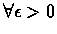
(If we assume that there is a state s such that
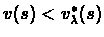 we pick
we pick
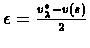 , and reach a contradiction)
, and reach a contradiction)
We now prove (2)
Since
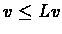 there exists a policy d such that
there exists a policy d such that
By theorem ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif)
Hence
Part (3) follows immediately from parts (1) and (2).




Next: The Solution of the
Up: Computing the Optimal Policy
Previous: Computing the Optimal Policy
Yishay Mansour
1999-11-24
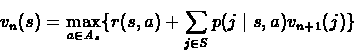
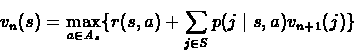
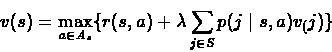
![]() ,
the right side of the
equality is at least as large as the left.
,
the right side of the
equality is at least as large as the left.
![]() and v we define
and v we define
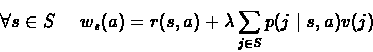
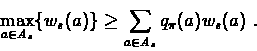
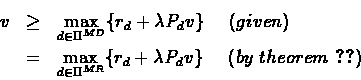
![\begin{eqnarray*}v & \geq &r_{d} + \lambda P_{d}v\\ & \geq & r_{d} + \lambda
P_...
...d})^{i}r_{d} + (\lambda P_{d})^{n}v \ \ \ (where\
[P^{0} = I])
\end{eqnarray*}](img72.gif)