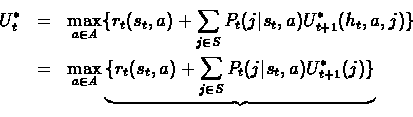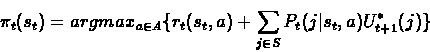Markovian Policy

Theorem 4.1   Let U_t^* be a solution to the optimality equations then

1.

For any t, 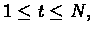$1 \leq t \leq N,$ U_t^*(h_t) depends on h_t only through s_t

2.

There exist a Markovian deterministic optimal policy

Proof:We will use a reversed induction to prove (1).
Basis: U_N^*(h_N)=r_N(s_N), therefore U_N^*(h_N)=U_N^*(s_N)
Induction Step: We assume the validity of the induction hypothesis for any n, $n \geq t+1$ and will prove the validity for t=n.

$$\begin{eqnarray*}U_t^* & = & \max_{a \in A} \{r_t(s_t,a) + \sum_{j\in S} P_t(j\v... ...{r_t(s_t,a) + \sum_{j\in S} P_t(j\vert s_t,a)U_{t+1}^*(j)\} }\\ \end{eqnarray*}$$

Note that the marked term depends merely on s and a. The entire term, therefore depends solely on s.
Thus,

U_t^*(h_t)=U_t^*(s_t)

To prove (2), let $\pi$ be a Markovian deterministic policy that sutisfies:

$${\pi}_t(s_t) = argmax_{a \in A} \{r_t(s_t,a) + \sum_{j\in S} P_t(j\vert s_t,a)U_{t+1}^*(j)\}$$

Since the policy's definition depends solely on s_t, namely the current state, ${\pi}_t$ is a Markovian policy.$\Box$