![\begin{displaymath}V^{\pi}_N (s) = E^{\pi}_s E_N [\sum_{i=1}^N r(X_t,Y_t)]\end{displaymath}](img76.gif)
assuming that the final value of all the states is equal to 0.
Let N be distributed geometricly with parameter
Lemma 4.2
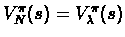
Under the assumption that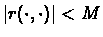
Under the assumption that
Proof:
![\begin{eqnarray*}V^{\pi}_N (s) & = & E^{\pi}_s \{\sum_{n=1}^\infty [\sum_{t=1}^n...
...^\infty \lambda^{t-1} r(X_t,Y_t)]\\
& = & V^{\pi}_{\lambda} (s)
\end{eqnarray*}](img80.gif)
The probablity to move into state
The sum of the immediate rewards from the new model is equal to the discounted sum of the immediate rewards from the original model.