![\begin{eqnarray*}V^{\pi}(s) & = & \lim_{N \rightarrow \infty} E_s^{\pi}[\sum_{t=...
...(X_t, Y_t)]\\
& = & \lim_{N \rightarrow \infty} V_N^{\pi}(s)\\
\end{eqnarray*}](img61.gif)
Note that this return function may diverge.
![\begin{displaymath}V_\lambda^{\pi}(s) = \lim_{N \rightarrow \infty} E_s^{\pi}[\sum_{t=1}^N \lambda^{t-1}r_t(X_t, Y_t)],\;\;\; 0 < \lambda < 1\end{displaymath}](img62.gif)
In this case, a suffice condition for convergence can be for example:
Under this condition we can find an upper bound to the return function:
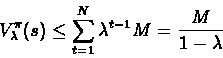
Note that this bound is very sensative to the value of the paramter
![\begin{eqnarray*}g^{\pi}(s) & = & \lim_{N \rightarrow \infty} \frac{1}{N} E^{\pi...
...)]\\
& = & \lim_{N \rightarrow \infty} \frac{1}{N} V^{\pi}_N(s)
\end{eqnarray*}](img67.gif)
This limit does not always exist. A sutisfactory demand for the limit's existance may be
- (a)
- S is finite
- (b)
-
 is Markovian and stationary
is Markovian and stationary
- (c)
- the system is non periodic