


Next: A Numeric Example
Up: Example: The Recruiting Problem
Previous: The Solution
Optimality Proof
We will now show that the described policy agrees with the optimality equations.
We start by showing that if there is a time 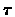 such that
such that
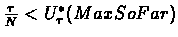 then
then
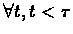 we get
we get
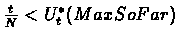 .
That is, if there exists a time
.
That is, if there exists a time 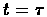 in
which it is preferred to Continue, then for each earlier time it is also preferred to continue. Later
on, we will show that such a time,
in
which it is preferred to Continue, then for each earlier time it is also preferred to continue. Later
on, we will show that such a time, 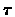 ,
does exist.
,
does exist.
Let
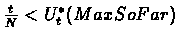 ,
then according to equation
,
then according to equation ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif)
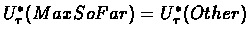 .
Performing backword induction steps, and using equations
.
Performing backword induction steps, and using equations ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) and
and ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) we show that for
we show that for
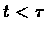 the inequality remains true:
the inequality remains true:
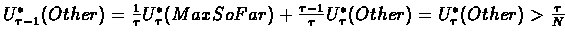
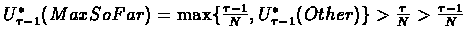
We now show that for 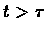 and
s=MaxSoFar, it is preferred to
QuitAndHire.
and
s=MaxSoFar, it is preferred to
QuitAndHire.
Let 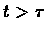 ,
then according to the first half of the proof,
,
then according to the first half of the proof,
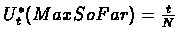
and,
We conclude this proof by showing that such a 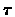 exists, that is, for
exists, that is, for 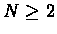 there exists
there exists
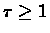 that meets the above requiremints. Let us assume
that meets the above requiremints. Let us assume 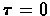 we get:
we get:
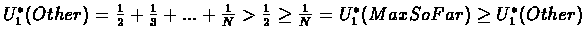
which is a circular inequality, and thus leads to cnotradiction.
Note that for 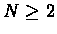 we always get
we always get
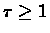 :
:
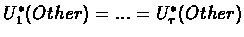
||
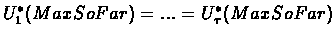
and for 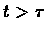
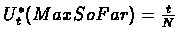
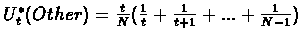 .
.
We therefore choose Continue if
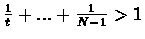 and
QuitAndHire otherwise.
and
QuitAndHire otherwise.



Next: A Numeric Example
Up: Example: The Recruiting Problem
Previous: The Solution
Yishay Mansour
1999-11-18
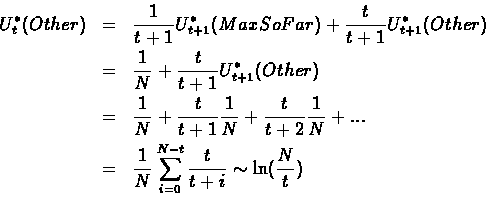
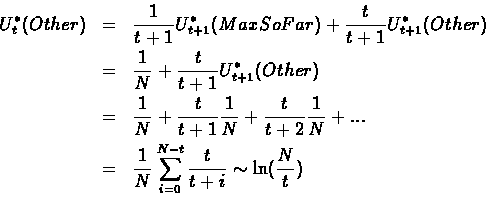
![]() exists, that is, for
exists, that is, for ![]() there exists
there exists
![]() that meets the above requiremints. Let us assume
that meets the above requiremints. Let us assume ![]() we get:
we get:
![]()
![]() we always get
we always get
![]() :
:
![]()
![]()
![]()
![]()
![]() .
.
![]() and
QuitAndHire otherwise.
and
QuitAndHire otherwise.