


Next: TD-Gammon
Up: TD-Gammon
Previous: methods of encoding
Choosing the parameters for F(r,s)
If it is
possible, we would like to find a vector r such that:
In most cases, it isn't possible since there aren't sufficient
computing resources. Therefore, we should discuss the distance
between F and 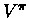 .
One way to measure this distance is to
calculate the minimum square error (MSE):
.
One way to measure this distance is to
calculate the minimum square error (MSE):
If it is possible to encode 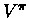 using F(r,s), this minimum
equals to 0. Otherwise, we try to get as close as possible to
using F(r,s), this minimum
equals to 0. Otherwise, we try to get as close as possible to
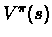 .
For linear functions it is sometimes possible to
compute
.
For linear functions it is sometimes possible to
compute
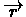 which minimizes the MSE, but
generally, it is a difficult task.
Let's look at the problem in the following manner: we try to
minimize
which minimizes the MSE, but
generally, it is a difficult task.
Let's look at the problem in the following manner: we try to
minimize
Finding the global minimum cannot always be done efficiently, and
it is much easier to find a local minimum (and hope it is good
enough).To find a local minimum, we can follow the derivative of
G(r,s). As long as the derivative is non zero, we have a
direction, in which G(r,s) is descending. When the value of the
derivative equals to zero, we are done. We now only need to
establish that this is a minimum (and not a maximum or an
inflection point). The reason that this is not a maximum value is
that the function descends to this point. However, we could be at
an inflection point, and remain there (because the derivative
could be fixed on zero in that neighborhood).
Recall that:
Of course, we don't have access to
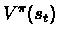 ,
but rather to a sample of it vt (which
could be noisy). Thus, we have:
,
but rather to a sample of it vt (which
could be noisy). Thus, we have:
For example, vt could be a Monte-Carlo estimate, i.e. the
total reward from time t onwards Rt.
In the case of backgammon, vt denotes whether we won or lost
the game. Similarly,



Next: TD-Gammon
Up: TD-Gammon
Previous: methods of encoding
Yishay Mansour
2000-01-17