


Next: methods of encoding
Up: TD-Gammon
Previous: MDP description
"Encoding" Functions
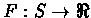
One way to implement F is by using a table. This enables us to implement any function F. The drawback in this
approach is that the space needed is proportional to the number of states. Since, in backgammon, the number of states is
very large (
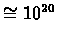 ), using a table is impractical.
We will implement F in way which does not enable any
mapping
), using a table is impractical.
We will implement F in way which does not enable any
mapping
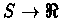 .
First, we choose a mapping
.
First, we choose a mapping
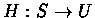 ,
which for each state s maps a vector
,
which for each state s maps a vector
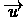 ,
which will "represent" it. Choosing such
appropriate mapping h determines the performance of the
algorithm. For example:
,
which will "represent" it. Choosing such
appropriate mapping h determines the performance of the
algorithm. For example:
- 1.
- TD-Gammon -
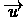 is a vector with 198 slots.
is a vector with 198 slots.
- 2.
- 21 (blackjack) - u is the sum of cards.
From here on, we exchange s with
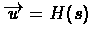 ,
and
perform the calculations on the vector
,
and
perform the calculations on the vector
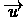 .
In the game of 21 there were few such vectors
.
In the game of 21 there were few such vectors
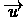 ,
and we could build a table for all of them.
It is not the case for backgammon.
,
and we could build a table for all of them.
It is not the case for backgammon.
Yishay Mansour
2000-01-17