


Next: "Encoding" Functions
Up: TD-Gammon
Previous: State encoding TD-Gammon
MDP
description
- 1.
- The discount factor is set to
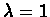 .
.
- 2.
- Immediate rewards:
- (a)
- In non-terminal states the immediate rewards are equal to 0.
- (b)
- In a winning terminal state the immediate reward equals 1.
- (c)
- In a losing terminal state the immediate reward equals 0.
I.e. the TD has a difference of
V(st+1) - V(st) for all
non-terminal states.
In every move the parameters are changed in the direction of the
TD. Generally, assume we have a function
F(s,r) = Vr(s)
,which gives each state s a value according to r (r is
actually a program which gets a state s as an input). We will
update
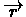 by the derivative of Vr(s)
according to
by the derivative of Vr(s)
according to
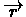 .
I.e. according to the vector
.
I.e. according to the vector
![$[\frac{\partial}{\partial r_{1}}V_{r}(s),\ldots
,\frac{\partial}{\partial r_{k}}V_{r}(s)]$](img9.gif) .
Updating
.
Updating
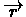 in this direction will hopefully change the
value of Vr(s) in the "right" direction. TD tries to minimize
the difference between two succeeding states: assuming that
Vr(st+1) > Vr(st), we would like to "strengthen" the
weight of the action taken, and update in the direction of
in this direction will hopefully change the
value of Vr(s) in the "right" direction. TD tries to minimize
the difference between two succeeding states: assuming that
Vr(st+1) > Vr(st), we would like to "strengthen" the
weight of the action taken, and update in the direction of
![$[V_{r}(s_{t+1}) - V_{r}(s_{t})]\nabla_{\overrightarrow{r}}
V_{t}(s_{t})$](img10.gif) For example, if r is a table:
For example, if r is a table:
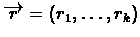 ,
then
,
then
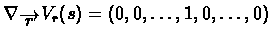 ,
and the update will occur only
in the s'th entry of r.
TD Gammon updates
,
and the update will occur only
in the s'th entry of r.
TD Gammon updates
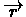 while running the system,
where the current policy is the greedy policy with respect to the
function Vr(s).
Specifically,
while running the system,
where the current policy is the greedy policy with respect to the
function Vr(s).
Specifically,
![$\overrightarrow{r_{t+1}} = \overrightarrow{r_{t}} +
\alpha[V_{t}(s_{t+1}) - V_{t}(s_{t})]\cdot\overrightarrow{e_{t}}$](img13.gif) ,
where
,
where
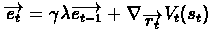 TD-Gammon simply "learns" by playing against itself, i.e it updated
TD-Gammon simply "learns" by playing against itself, i.e it updated
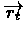 while playing against itself.
After about 300,000 games the system achieved a very good
playing skill (equivalent to other backgammon playing programs).
while playing against itself.
After about 300,000 games the system achieved a very good
playing skill (equivalent to other backgammon playing programs).



Next: "Encoding" Functions
Up: TD-Gammon
Previous: State encoding TD-Gammon
Yishay Mansour
2000-01-17