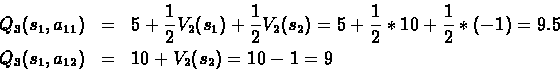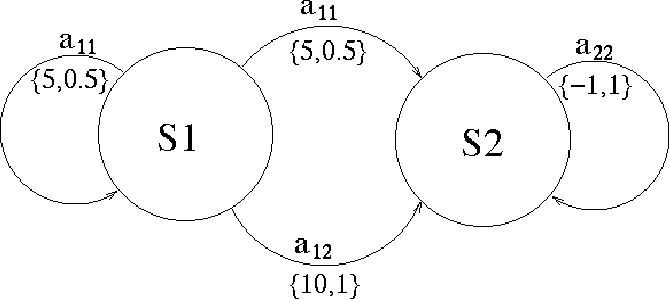
Example 2

 

Figure: State Diagram

Lets define a state machine with two states s₁, s₂.

Formally, in the example we have:

time: $T=\{1...N\}$

states: $S = \{s_1,s_2\}$

actions: $A_{s_1}=\{a_{11}, a_{12}\}, A_{s_2}=\{a_{21}\}$

reward: r_t(s₁,a₁₁) = 5, r_t(s₁,a₁₂) = 10, r_t(s₂,a₂₁) = -1

final reward: r_N(s₁) = 0, r_N(s₂) = 0

transition function: P_t(s₁|s₁,a₁₁) = 0.5, P_t(s₂|s₁,a₁₁) = 0.5

P_t(s₂|s₁,a₁₂) = 1, P_t(s₂|s₂,s₂₁) = 1

Now we want to maximize the return. First we compare two deterministic policies:

$\pi_1$- always chooses a₁₁ when in state s₁.

$\pi_2$ - always chooses a₁₂ when in state s₂.

Recall that $V_N(\Pi)$ is the expected return of policy $\Pi$ in N time steps.

$$\begin{eqnarray*}V_3(\pi_1) & = & \frac{1}{2}(5-1+0) +\frac{1}{2}(5+5+0)=7 \\ V... ...{4}(10-2)+\frac{1}{8}(20) = 7.25 \\ V_5(\pi_2) & = & 10 - 3 = 7 \end{eqnarray*}$$

Notice how in shorter time frames $\pi_2$ is the preferable policy, while in longer ones, $\pi_1$ brings on the higher returns.

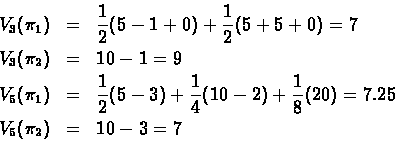
Lets try determining the best policy. We do this by looking first at the reward gained in the last step, for N=2:

$$\begin{eqnarray*}Q_2(s_1,a_{11}) & = & 5 \\ Q_2(s_1,a_{12}) & = &10 \end{eqnarray*}$$

In this case:

$$\begin{eqnarray*}V_2(s_1) & = & 10 \\ V_2(s_2) & = & -1 \end{eqnarray*}$$

When N=2, The optimal action from s₁ is a₁₂.

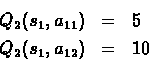
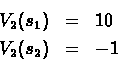
For N=3, we use the optimal policy for N=2, after we do one action.

$$\begin{eqnarray*}Q_3(s_1,a_{11}) & = & 5+\frac{1}{2}V_2(s_1)+\frac{1}{2}V_2(s_2)... ...}*(-1) = 9.5 \\ Q_3(s_1,a_{12}) & = & 10+ V_2(s_2) = 10 - 1 = 9 \end{eqnarray*}$$

Hence, when N=3 the optimal action from s₁ is a₁₁.