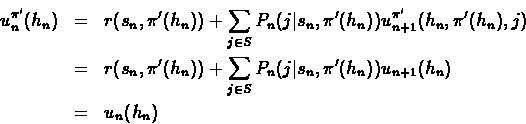Let us define:
![]() .
For the simplicity of the discussion we assume that both S and A are finite.
The optimality equations (also known as Bellman equations) are:
.
For the simplicity of the discussion we assume that both S and A are finite.
The optimality equations (also known as Bellman equations) are:
![]()
Where UN(hN)=rN(sN) for hN=(hN-1,aN-1,sN).
Note that replacing the max operation in the equation with the action taken by policy ![]() ,
we get the equation for computing the return of policy
,
we get the equation for computing the return of policy ![]() .
.
(1)
![]()
(2)
![]()
Proof:First, we will show by induction that
![]() for
for
![]() and for every
and for every
![]() .
Then we exhibit a specific policy
.
Then we exhibit a specific policy ![]() for which
for which
![]() and that this will conclude the proof.
and that this will conclude the proof.
Basis: When t=N, by definition
![]() for every policy
for every policy ![]() and therefore
uN(hN)=u*N(hN).
and therefore
uN(hN)=u*N(hN).
Induction Step: Let us assume that
![]() for
for
![]() and
and
![]() .
Let
.
Let ![]() be a policy in
be a policy in ![]() (that performs the operation dn' on step n). for t=n:
(that performs the operation dn' on step n). for t=n:
![]()
Consider an arbitrary policy ![]() ,
that for history hn uses stochastic action q(a). By the induction assumption,
,
that for history hn uses stochastic action q(a). By the induction assumption,
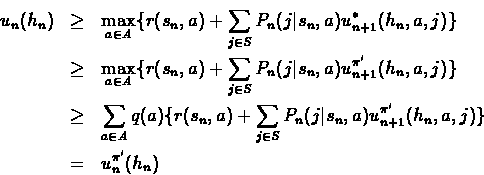
![]()
We will now show that
![]() using reversed induction on n.
using reversed induction on n.
Basis: for n=N this is obviously true.
Induction Step: